Skip over navigation
Answer: 24
Using equivalent ratios
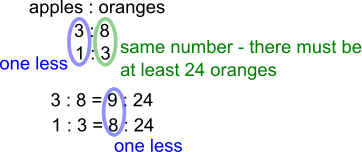
Using multiples
At the beginning, there are 8 oranges for every 3 apples, so the number of oranges must be a multiple of 8.
At the end, there are 3 oranges for every apple, so the number of oranges must be a multiple of 3.
The number of oranges does not change, so it must be a multiple of 8 and a multiple of 3. Common multiples of 3 and 8 are 24, 48, ... so we could try these as the number of oranges.
3 : 8 is equivalent to 9 : 24
1 : 3 is equivalent to 8 : 24
9 $-$ 1 = 8, so there were 9 apples and 24 oranges to begin with.
Using algebra
Let $a$ be the number of apples and $o$ be the number of oranges at the beginning. Then we have that the ratio $a:o$ is $3:8$ and the ratio $a-1:o$ is $1:3.$
These give the simultaneous equations $8a=3o$ and $3(a-1)=o\Rightarrow 3a-3=o$
Solving by elimination
Multiplying both sides of $3a-3=o$ by $3$ gives $9a-9=3o$. Subtracting the equation $8a=3o$ from $9a-9=3o$ gives $$\begin{align}9a-9-8a&=3o-3o\\\Rightarrow a-9&=0\\\Rightarrow a&=9\end{align}$$
Substituting $a=9$ into $3a-3=o$ gives $o=3\times9-3=24.$
Solving by substitution
Substituting $o=3a-3$ into $8a=3o$ gives $$\begin{align}8a&=3(3a-3)\\
\Rightarrow8a&=9a-9\\
\Rightarrow0&=a-9\\
\Rightarrow9&=a\end{align}$$
Substituting $a=9$ into $3a-3=o$ gives $o=3\times9-3=24.$

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Fruit Basket Ratio
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
Answer: 24
Using equivalent ratios
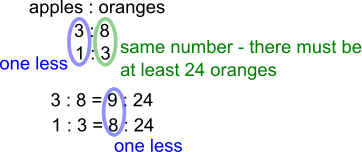
Using multiples
At the beginning, there are 8 oranges for every 3 apples, so the number of oranges must be a multiple of 8.
At the end, there are 3 oranges for every apple, so the number of oranges must be a multiple of 3.
The number of oranges does not change, so it must be a multiple of 8 and a multiple of 3. Common multiples of 3 and 8 are 24, 48, ... so we could try these as the number of oranges.
3 : 8 is equivalent to 9 : 24
1 : 3 is equivalent to 8 : 24
9 $-$ 1 = 8, so there were 9 apples and 24 oranges to begin with.
Using algebra
Let $a$ be the number of apples and $o$ be the number of oranges at the beginning. Then we have that the ratio $a:o$ is $3:8$ and the ratio $a-1:o$ is $1:3.$
These give the simultaneous equations $8a=3o$ and $3(a-1)=o\Rightarrow 3a-3=o$
Solving by elimination
Multiplying both sides of $3a-3=o$ by $3$ gives $9a-9=3o$. Subtracting the equation $8a=3o$ from $9a-9=3o$ gives $$\begin{align}9a-9-8a&=3o-3o\\\Rightarrow a-9&=0\\\Rightarrow a&=9\end{align}$$
Substituting $a=9$ into $3a-3=o$ gives $o=3\times9-3=24.$
Solving by substitution
Substituting $o=3a-3$ into $8a=3o$ gives $$\begin{align}8a&=3(3a-3)\\
\Rightarrow8a&=9a-9\\
\Rightarrow0&=a-9\\
\Rightarrow9&=a\end{align}$$
Substituting $a=9$ into $3a-3=o$ gives $o=3\times9-3=24.$
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.

