Perimeter in a Hexagon

Using an equilateral tiangle and a parallelogram
In the diagram below, the red line connects two of the hexagon's vertices. Since it is parallel to the top and bottom sides, and the sides of the grey triangle are parallel to the sides of the hexagon, the blue shape is an equilateral triangle and the green shape is a parallelogram.
 
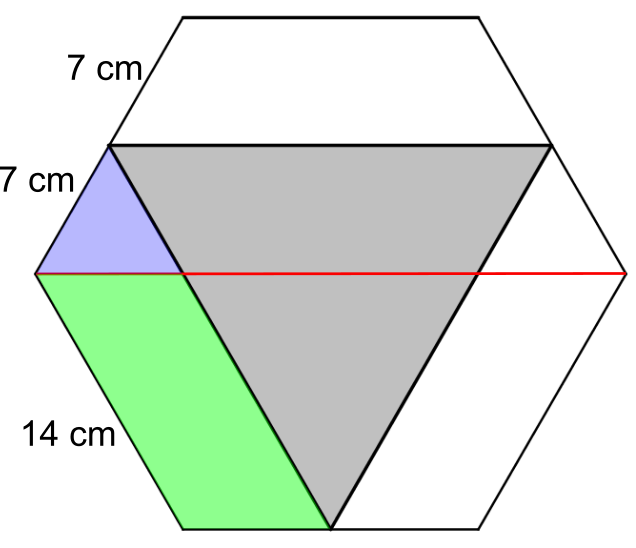
That means we can label some lengths on the grey triangle:
 
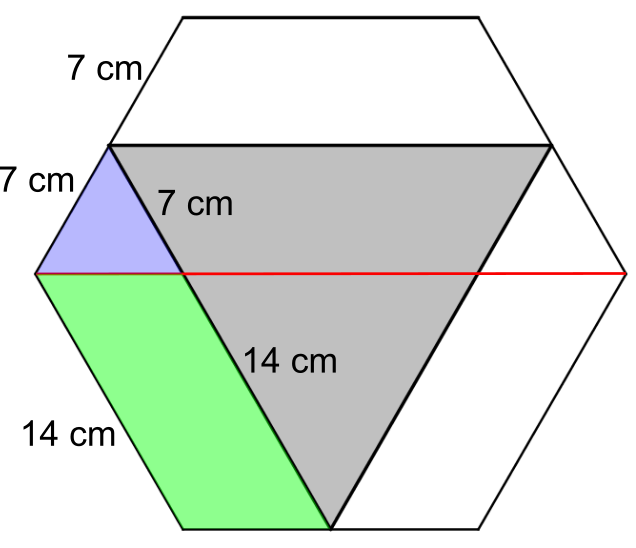
So the side length of the grey triangle is 7 + 14 = 21 cm, so its perimeter is 21 $\times$ 3 = 63 cm.


Using lots of little triangles
We can split the hexagon up into smaller equilateral triangles as shown:

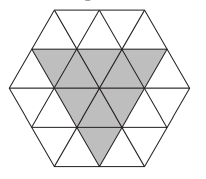
There are two small triangles along each side of the hexagon, so the side length of each small triangle is half of 14 cm, which is 7 cm.

There are three small triangles along each side of the shaded triangle, so the side length of the shaded triangle is 3 $\times$ 7 = 21 cm. So its perimeter is 21 $\times$ 3 = 63 cm.