Skip over navigation
Using circle theorems
By the circle theorem that angles at the circumference drawn from the same chord are always equal, the point C can be moved around the circumference, such as from C to C' in the diagram below, without changing the angle ACB (marked $x$).
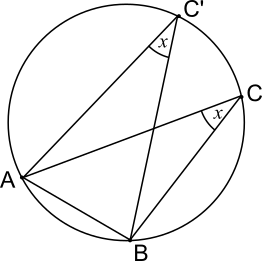
This means that we can choose to put point C diametrically opposite point A, as shown below.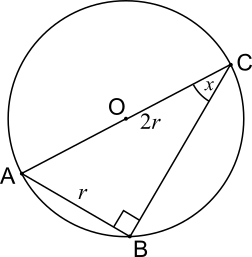
Now, triangle ABC is right-angled because it is a triangle in a semicircle, and since AB is equal to the radius and AC is equal to the diameter, they can be labelled $r$ and $2r$.
Notice that $\triangle OAB$ is equilateral so $\angle OAB=60^{\circ}$ so $\angle ACB=30^{\circ}$.
Or we could use Trigonometry:
$\sin x = \dfrac{\text{opp}}{\text{hyp}}=\dfrac{r}{2r}=\dfrac12$, so $x=30^{\circ}$.
If you are unfamiliar with circle theorems, you can work it out as follows:
Using radii and triangles
In the diagrams below, O is the centre of the circle. The line segments AC, AO, BO and CO have been added. All of the red segments are radii, or AB which is equal to the radius, so they are all equal. Two possible positions for the point C are shown.

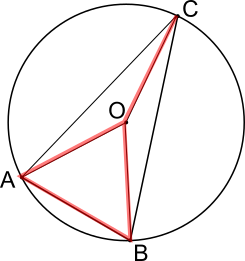
ABO is an equilateral triangle, so all of its angles are 60$^\text o$. ACO and BCO are isosceles, and their equal angles are marked x and y respectively in the diagrams below. In the diagram on the left, CAB is 60$^\text o$- x and ACB is y - x because the line AC divides the angles OAB and OCB.


The sum of the angles in triangle ABC is 180$^\text o$.
Using the triangle on the right, angle ACB is x + y, and x + 60$^\text o$ + 60$^\text o$ + y + y + x = 180$^\text o$.
This simplifies to 2x + 2y + 120$^\text o$ = 180$^\text o$, so 2(x + y) = 60$^\text o$, so x + y = 30$^\text o$.
Using the triangle on the left, angle ACB is y - x, and 60$^\text o$ - x + 60$^\text o$ + y + y - x = 180$^\text o$.
This simplifies to 120$^\text o$ + 2y - 2x = 180$^\text o$, so 2(y - x) = 60$^\text o$, so y - x = 30$^\text o$.
So angle ACB is 30$^\text o$.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Circular Inscription
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Using circle theorems
By the circle theorem that angles at the circumference drawn from the same chord are always equal, the point C can be moved around the circumference, such as from C to C' in the diagram below, without changing the angle ACB (marked $x$).

This means that we can choose to put point C diametrically opposite point A, as shown below.

Now, triangle ABC is right-angled because it is a triangle in a semicircle, and since AB is equal to the radius and AC is equal to the diameter, they can be labelled $r$ and $2r$.
Notice that $\triangle OAB$ is equilateral so $\angle OAB=60^{\circ}$ so $\angle ACB=30^{\circ}$.
Or we could use Trigonometry:
$\sin x = \dfrac{\text{opp}}{\text{hyp}}=\dfrac{r}{2r}=\dfrac12$, so $x=30^{\circ}$.
If you are unfamiliar with circle theorems, you can work it out as follows:
Using radii and triangles
In the diagrams below, O is the centre of the circle. The line segments AC, AO, BO and CO have been added. All of the red segments are radii, or AB which is equal to the radius, so they are all equal. Two possible positions for the point C are shown.


ABO is an equilateral triangle, so all of its angles are 60$^\text o$. ACO and BCO are isosceles, and their equal angles are marked x and y respectively in the diagrams below. In the diagram on the left, CAB is 60$^\text o$- x and ACB is y - x because the line AC divides the angles OAB and OCB.


The sum of the angles in triangle ABC is 180$^\text o$.
Using the triangle on the right, angle ACB is x + y, and x + 60$^\text o$ + 60$^\text o$ + y + y + x = 180$^\text o$.
This simplifies to 2x + 2y + 120$^\text o$ = 180$^\text o$, so 2(x + y) = 60$^\text o$, so x + y = 30$^\text o$.
Using the triangle on the left, angle ACB is y - x, and 60$^\text o$ - x + 60$^\text o$ + y + y - x = 180$^\text o$.
This simplifies to 120$^\text o$ + 2y - 2x = 180$^\text o$, so 2(y - x) = 60$^\text o$, so y - x = 30$^\text o$.
So angle ACB is 30$^\text o$.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
Bendy Quad
Four rods are hinged at their ends to form a convex quadrilateral. Investigate the different shapes that the quadrilateral can take. Be patient this problem may be slow to load.

