Skip over navigation
Using a two-way table and ratios
b = 0
Ratio of c:d = 1:9
d = 54% of total
so c = 6% of total
so a must be the remaining 40% of total
So 40% voted for the Broccoli Party.
Using a two-way table and equations
The information can be shown in a two-way table, where $x\%$ of voters voted for the Broccoli party and $y\%$ of voters voted for other parties:
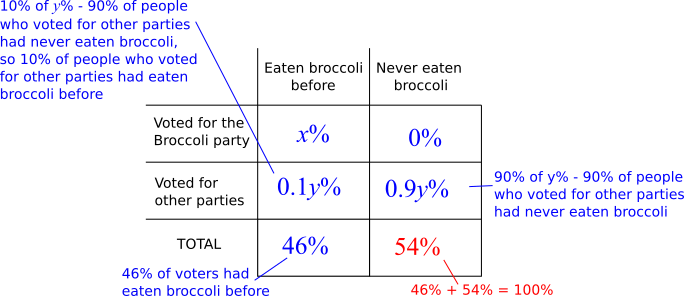
From the 'Never eaten broccoli' column, $0+0.9y=54$, so $y=54\div0.9=60$.
$x+y=100$ so $x=40$. So $40\%$ of voters voted for the Broccoli party.
Using a tree diagram
Some of the information from the question is shown on the tree diagram below:

$46\%$ of voters had eaten broccoli before, so $100\%$ of $x$ added to $10\%$ of $y$ is $46,$ so $x+0.1y=46$.
All voters either voted for the Broccoli party or for another party, so $x+y=100$.
Solving by elimination
Subtracting $x+0.1y=46$ from $x+y=100$ gives $$\begin{align}x+y-(x+0.1y)=&100-46\\
\Rightarrow x+y-x-0.1y=&54\\
\Rightarrow 0.9y=&54\\
\Rightarrow y=&54\div0.9=60\end{align}$$ So 60% of voters voted for other parties, so 40% of voters voted for the Broccoli party.
Solving by substitution
$x+y=100\Rightarrow y=100-x$. Substituting this into $x+0.1y=46$ gives $$\begin{align}x+0.1(100-x)&=46\\
\Rightarrow x+ 10 - 0.1x&=46\\
\Rightarrow 0.9x&=36\\
\Rightarrow x&=36\div0.9=40\end{align}$$



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Vegtown Elections
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Using a two-way table and ratios
| Ate broccoli | Never ate broccoli | |
| Voted Broccoli party | a | b |
| Voted for other parties | c | d |
b = 0
Ratio of c:d = 1:9
d = 54% of total
so c = 6% of total
so a must be the remaining 40% of total
So 40% voted for the Broccoli Party.
Using a two-way table and equations
The information can be shown in a two-way table, where $x\%$ of voters voted for the Broccoli party and $y\%$ of voters voted for other parties:

From the 'Never eaten broccoli' column, $0+0.9y=54$, so $y=54\div0.9=60$.
$x+y=100$ so $x=40$. So $40\%$ of voters voted for the Broccoli party.
Using a tree diagram
Some of the information from the question is shown on the tree diagram below:

$46\%$ of voters had eaten broccoli before, so $100\%$ of $x$ added to $10\%$ of $y$ is $46,$ so $x+0.1y=46$.
All voters either voted for the Broccoli party or for another party, so $x+y=100$.
Solving by elimination
Subtracting $x+0.1y=46$ from $x+y=100$ gives $$\begin{align}x+y-(x+0.1y)=&100-46\\
\Rightarrow x+y-x-0.1y=&54\\
\Rightarrow 0.9y=&54\\
\Rightarrow y=&54\div0.9=60\end{align}$$ So 60% of voters voted for other parties, so 40% of voters voted for the Broccoli party.
Solving by substitution
$x+y=100\Rightarrow y=100-x$. Substituting this into $x+0.1y=46$ gives $$\begin{align}x+0.1(100-x)&=46\\
\Rightarrow x+ 10 - 0.1x&=46\\
\Rightarrow 0.9x&=36\\
\Rightarrow x&=36\div0.9=40\end{align}$$
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Gambling at Monte Carlo
A man went to Monte Carlo to try and make his fortune. Is his strategy a winning one?
Marbles and Bags
Two bags contain different numbers of red and blue marbles. A marble is removed from one of the bags. The marble is blue. What is the probability that it was removed from bag A?
Coin Tossing Games
You and I play a game involving successive throws of a fair coin. Suppose I pick HH and you pick TH. The coin is thrown repeatedly until we see either two heads in a row (I win) or a tail followed by a head (you win). What is the probability that you win?

