Skip over navigation
Answer: 11
Using algebra
Since we are looking for the largest of the eight integers, let the largest one be $n$. Then the others are $n-1$, $n-2$ and so on, and we are given that
$$\begin{align}n+(n-1)+(n-2)&=(n-3)+(n-4) +(n-5)+(n-6)+(n-7)\\
\Rightarrow 3n-1-2&=5n-3-4-5-6-7\\
\Rightarrow 3n-3&=5n-25\\
\Rightarrow3n+22&=5n\\
\Rightarrow 22&=2n\\
\Rightarrow 11&=n\end{align}$$ So the largest number is $11$.
Looking for patterns between choices
Compare starting from 1, 2, ... 8
with starting from 2, 1, ... 9
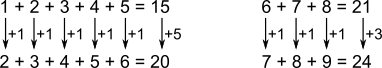
This will keep happening:
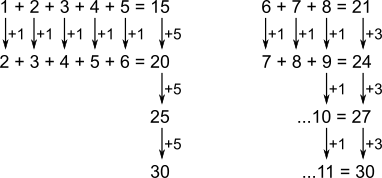
So the largest of the integers is 11.
(Check: 4 + 5 + 6 + 7 + 8 = 30; 9 + 10 + 11 = 30)
Looking for patterns between the numbers
Look at the differences between the last three numbers in the first five, and the second three numbers.
8 is 1 more than 7, 9 is 3 more than 6 and 10 is 5 more than 5.
Sliding the red boxes to the left or right along the number line will change the numbers in the boxes, but not the differences between the numbers.

This means that wherever the red boxes are placed, the difference between the last three numbers in the first five and the second three numbers will always be the same.
That difference will always be 1 + 3 + 5 = 9.
So to balance out the sums, the first two numbers must add up to 9.
Since they are consecutive, they must be 4 and 5. So the numbers are 4, 5, 6, 7, 8 and 9, 10, 11 - and the largest number is 11.
(Check: 4 + 5 + 6 + 7 + 8 = 30; 9 + 10 + 11 = 30)


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
8 in a Row
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
Answer: 11
Using algebra
Since we are looking for the largest of the eight integers, let the largest one be $n$. Then the others are $n-1$, $n-2$ and so on, and we are given that
$$\begin{align}n+(n-1)+(n-2)&=(n-3)+(n-4) +(n-5)+(n-6)+(n-7)\\
\Rightarrow 3n-1-2&=5n-3-4-5-6-7\\
\Rightarrow 3n-3&=5n-25\\
\Rightarrow3n+22&=5n\\
\Rightarrow 22&=2n\\
\Rightarrow 11&=n\end{align}$$ So the largest number is $11$.
Looking for patterns between choices
Compare starting from 1, 2, ... 8
with starting from 2, 1, ... 9
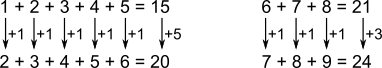
This will keep happening:
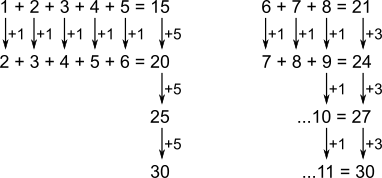
So the largest of the integers is 11.
(Check: 4 + 5 + 6 + 7 + 8 = 30; 9 + 10 + 11 = 30)
Looking for patterns between the numbers
Look at the differences between the last three numbers in the first five, and the second three numbers.
8 is 1 more than 7, 9 is 3 more than 6 and 10 is 5 more than 5.
Sliding the red boxes to the left or right along the number line will change the numbers in the boxes, but not the differences between the numbers.

This means that wherever the red boxes are placed, the difference between the last three numbers in the first five and the second three numbers will always be the same.
That difference will always be 1 + 3 + 5 = 9.
So to balance out the sums, the first two numbers must add up to 9.
Since they are consecutive, they must be 4 and 5. So the numbers are 4, 5, 6, 7, 8 and 9, 10, 11 - and the largest number is 11.
(Check: 4 + 5 + 6 + 7 + 8 = 30; 9 + 10 + 11 = 30)
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...

