Skip over navigation
Answer: 35 km/h
Using a speed-time graph


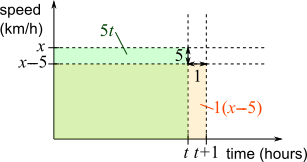
$\therefore 5t = x-5$ and $xt=210$
$5t = x-5\Rightarrow t = \frac{x-5}5$
$xt = 210 \Rightarrow x\left(\frac{x-5}5\right)=210\\
\hspace{18mm}\Rightarrow x(x-5)=1050\\
\hspace{18mm}\Rightarrow x^2-5x-1050=0$
The quadratic formula gives: $$\begin{align}x&=\frac{5\pm\sqrt{25--4200}}2\\
&=\frac{5\pm\sqrt{169\times25}}2\\
&=\frac{5\pm65}2\end{align}$$ So $x=35$
Using time = distance $\div$ speed
Average speed over $210$ km is $x$ km/h, then time is $\dfrac{210}x$ hours.
Planned average speed is $x-5$ km/h, time at planned speed $\dfrac{210}{x-5}$ hours.
$1$ hour earlier than planned, so $\dfrac{210}x$ is $1$ less than $\dfrac{210}{x-5}$, so $$\begin{align}&\frac{210}{x}=\frac{210}{x-5}-1\\ \hspace{1mm}\\
\Rightarrow&210=\frac{210x}{x-5}-x\\\hspace{1mm}\\
\Rightarrow&210(x-5)=210x-x(x-5)\\
\Rightarrow&210x-1050=210x-x^2+5x\\
\Rightarrow&x^2-5x-1050=0\\
\Rightarrow&(x+30)(x-35)=0\end{align}$$ So $x=-30$ or $x=35$. Since $x>0, x=35$.
Using distance = speed $\times$ time
If Chris completed the journey in $t$ hours, distance $=x\times t$.
Chris intended to take $t+1$ hours.
He intended to travel $5$ km/h slower, so at an average speed of $x-5$ km/h.
Distance $=(x-5)(t+1)=xt-5t+x-5$
Distances are the same so $xt = xt-5t+x-5\Rightarrow0=-5t+x-5\Rightarrow x=5t+5$
And $xt=210$ so $(5t+5)t=210\Rightarrow (t+1)t=42$ so $t, t+1$ could be $6,7$ (or $-6, -7$)
$x=5\times6+5=35$

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Day Out
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Answer: 35 km/h
Using a speed-time graph



$\therefore 5t = x-5$ and $xt=210$
$5t = x-5\Rightarrow t = \frac{x-5}5$
$xt = 210 \Rightarrow x\left(\frac{x-5}5\right)=210\\
\hspace{18mm}\Rightarrow x(x-5)=1050\\
\hspace{18mm}\Rightarrow x^2-5x-1050=0$
The quadratic formula gives: $$\begin{align}x&=\frac{5\pm\sqrt{25--4200}}2\\
&=\frac{5\pm\sqrt{169\times25}}2\\
&=\frac{5\pm65}2\end{align}$$ So $x=35$
Using time = distance $\div$ speed
Average speed over $210$ km is $x$ km/h, then time is $\dfrac{210}x$ hours.
Planned average speed is $x-5$ km/h, time at planned speed $\dfrac{210}{x-5}$ hours.
$1$ hour earlier than planned, so $\dfrac{210}x$ is $1$ less than $\dfrac{210}{x-5}$, so $$\begin{align}&\frac{210}{x}=\frac{210}{x-5}-1\\ \hspace{1mm}\\
\Rightarrow&210=\frac{210x}{x-5}-x\\\hspace{1mm}\\
\Rightarrow&210(x-5)=210x-x(x-5)\\
\Rightarrow&210x-1050=210x-x^2+5x\\
\Rightarrow&x^2-5x-1050=0\\
\Rightarrow&(x+30)(x-35)=0\end{align}$$ So $x=-30$ or $x=35$. Since $x>0, x=35$.
Using distance = speed $\times$ time
If Chris completed the journey in $t$ hours, distance $=x\times t$.
Chris intended to take $t+1$ hours.
He intended to travel $5$ km/h slower, so at an average speed of $x-5$ km/h.
Distance $=(x-5)(t+1)=xt-5t+x-5$
Distances are the same so $xt = xt-5t+x-5\Rightarrow0=-5t+x-5\Rightarrow x=5t+5$
And $xt=210$ so $(5t+5)t=210\Rightarrow (t+1)t=42$ so $t, t+1$ could be $6,7$ (or $-6, -7$)
$x=5\times6+5=35$
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like

Percentage Unchanged
If the base of a rectangle is increased by 10% and the area is unchanged, by what percentage is the width decreased by ?

