Skip over navigation
Using a table of values
Points in the first quadrant have $x,\hspace{2mm}y>0$, so we could begin by substituting values into the equation of the line to check for lattice points on the line.
Using the table below, we can try positive whole numbers for $x$, and then find the value of $3x$. If $x=1$, then $3x=3$, so $4y$ must be $56$ since $3+56=59$, so $y=56\div 4=14$. So the point $(1,14)$ lies on the line and is a lattice point. This is shown on the first line of the table.
If $x=2$, then $3x=6$, so $4y$ must be $53$ since $6+53=59$, so $y=53\div 4=13.25$. So the point $(2,13.25)$ lies on the line, but it is not a lattice point.
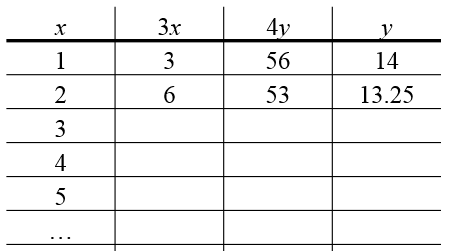
Filling in the whole table will give all of the possible lattice points. Remember that $y$ needs to be positive, so $3x$ must not be greater than $59$, so $x$ must be less than $20$ (since $3\times 20=60>59$). So the table only needs to go up to $x=19$.
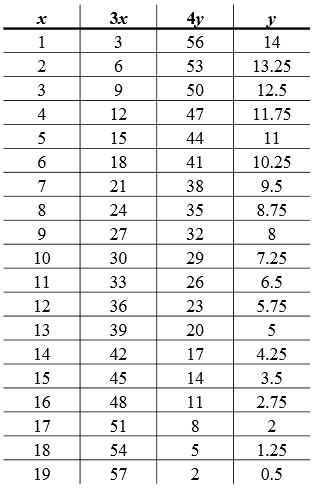
Counting the points in the table with whole number $y$ coordinates, there are 5 lattice points. Plotting these points gives the graph below (the lattice points are marked in red).
Using gradient triangles
The gradient of the line is $-\frac{3}{4}$. You can work this out by considering changes in $x$ and $y,$ or by rearranging $3x+4y=59$ into $y=-\frac{3x}{4}+\frac{59}{4}$.
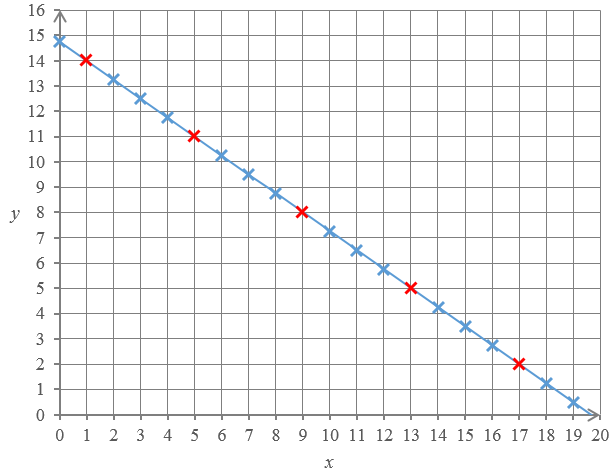
This means that every time $x$ increases by $4$, $y$ decreases by $3$. This is shown on the diagram below.
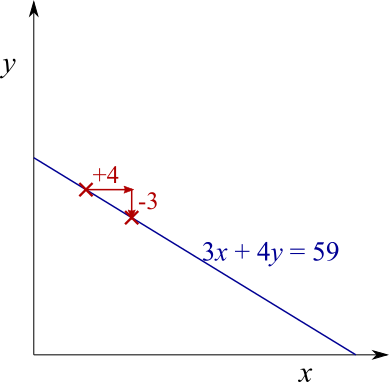
So, if you start at a lattice point, then there will be another lattice point $4$ to the left and $3$ down, and another one $8$ to the left and $6$ down, and so on. There will also be another lattice point $4$ to the right and $3$ up, and so on. So the lattice points, if there are any, will be evenly spaced along the $x$-axis at intervals of $4$, as shown below - where this time, we assume that the dark red crosses mark lattice points.
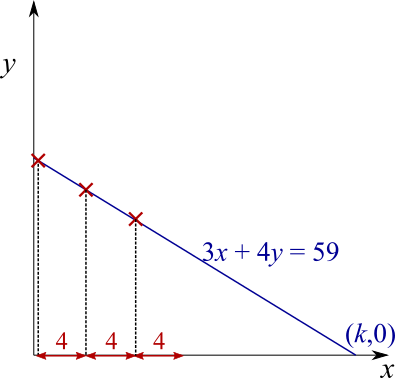
That means that, if we can find a lattice point on the line between $x=0$ and $x=4$, then we can quickly find all of the lattice points by adding $4$ to the $x$ coordinate until we get to $k$ (where $k$ is the $x$-intercept, as shown above).
However, if we can't find a lattice point between $x=0$ and $x=4$, then there won't be any lattice points at all, because lattice points should be at intervals of $4$, so there can't be an interval of $4$ that doesn't contain one.
If $x=1$, then $3x=3$, so $4y$ must be $56$ since $3+56=59$, so $y=56\div 4=14$. So the point $(1,14)$ lies on the line and is a lattice point.
Then there are also lattice points when $x=5, 9, 13 ”¦$. To work out how many there are in the first quadrant, we need to find the value of $k$, because if $x>k$ then the lattice point will not be in the first quadrant. When $x=k$, $y=0$, and so $3\times k+4\times 0=59$, so $k=59/3=19\frac{2}{3}$.
So the lattice points have $x$-coordinates $1, 5, 9, 13$ and $17$ - which means there are $5$ lattice points.
Using factorisation and properties of numbers
Suppose $(a,b)$ is lattice point on the line $3x+4y=59$ in the first quadrant. Then $a$ and $b$ are positive whole numbers with $3a+4b=59$.
$3a+4b$ can be written as $3(a+b)+b$. This is useful because, starting from $3(a+b)+b=59$, $3(a+b)=59-b$, so $59-b$ must be a multiple of $3$.
Also, since $a$ is positive, $3a$ is also positive, and so $4b<59$, so $b<59\div4$, so $b<14.75$, so $b\le 14$, since $b$ is a whole number.
That means that $59-b\ge 59-14$, so $59-b\ge 45$.
So $59-b$ is a multiple of $3$ that is between $45$ and $59$ ($b>0$ so $59-b<59$). So $59-b$ could be $45, 48, 51, 54$ or $57$. From each of those $5$ options, we can find $b$, and then $a+b$, and then $a$. So there are $5$ lattice points which satisfy the equation - so there are $5$ lattice points on the line.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Lattice Points on a Line
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
Using a table of values
Points in the first quadrant have $x,\hspace{2mm}y>0$, so we could begin by substituting values into the equation of the line to check for lattice points on the line.
Using the table below, we can try positive whole numbers for $x$, and then find the value of $3x$. If $x=1$, then $3x=3$, so $4y$ must be $56$ since $3+56=59$, so $y=56\div 4=14$. So the point $(1,14)$ lies on the line and is a lattice point. This is shown on the first line of the table.
If $x=2$, then $3x=6$, so $4y$ must be $53$ since $6+53=59$, so $y=53\div 4=13.25$. So the point $(2,13.25)$ lies on the line, but it is not a lattice point.
Filling in the whole table will give all of the possible lattice points. Remember that $y$ needs to be positive, so $3x$ must not be greater than $59$, so $x$ must be less than $20$ (since $3\times 20=60>59$). So the table only needs to go up to $x=19$.
Counting the points in the table with whole number $y$ coordinates, there are 5 lattice points. Plotting these points gives the graph below (the lattice points are marked in red).
Using gradient triangles
The gradient of the line is $-\frac{3}{4}$. You can work this out by considering changes in $x$ and $y,$ or by rearranging $3x+4y=59$ into $y=-\frac{3x}{4}+\frac{59}{4}$.
This means that every time $x$ increases by $4$, $y$ decreases by $3$. This is shown on the diagram below.

So, if you start at a lattice point, then there will be another lattice point $4$ to the left and $3$ down, and another one $8$ to the left and $6$ down, and so on. There will also be another lattice point $4$ to the right and $3$ up, and so on. So the lattice points, if there are any, will be evenly spaced along the $x$-axis at intervals of $4$, as shown below - where this time, we assume that the dark red crosses mark lattice points.

That means that, if we can find a lattice point on the line between $x=0$ and $x=4$, then we can quickly find all of the lattice points by adding $4$ to the $x$ coordinate until we get to $k$ (where $k$ is the $x$-intercept, as shown above).
However, if we can't find a lattice point between $x=0$ and $x=4$, then there won't be any lattice points at all, because lattice points should be at intervals of $4$, so there can't be an interval of $4$ that doesn't contain one.
If $x=1$, then $3x=3$, so $4y$ must be $56$ since $3+56=59$, so $y=56\div 4=14$. So the point $(1,14)$ lies on the line and is a lattice point.
Then there are also lattice points when $x=5, 9, 13 ”¦$. To work out how many there are in the first quadrant, we need to find the value of $k$, because if $x>k$ then the lattice point will not be in the first quadrant. When $x=k$, $y=0$, and so $3\times k+4\times 0=59$, so $k=59/3=19\frac{2}{3}$.
So the lattice points have $x$-coordinates $1, 5, 9, 13$ and $17$ - which means there are $5$ lattice points.
Using factorisation and properties of numbers
Suppose $(a,b)$ is lattice point on the line $3x+4y=59$ in the first quadrant. Then $a$ and $b$ are positive whole numbers with $3a+4b=59$.
$3a+4b$ can be written as $3(a+b)+b$. This is useful because, starting from $3(a+b)+b=59$, $3(a+b)=59-b$, so $59-b$ must be a multiple of $3$.
Also, since $a$ is positive, $3a$ is also positive, and so $4b<59$, so $b<59\div4$, so $b<14.75$, so $b\le 14$, since $b$ is a whole number.
That means that $59-b\ge 59-14$, so $59-b\ge 45$.
So $59-b$ is a multiple of $3$ that is between $45$ and $59$ ($b>0$ so $59-b<59$). So $59-b$ could be $45, 48, 51, 54$ or $57$. From each of those $5$ options, we can find $b$, and then $a+b$, and then $a$. So there are $5$ lattice points which satisfy the equation - so there are $5$ lattice points on the line.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
Related Collections
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...

