Scalene Area

Drawing lines from O to each vertex
Drawing lines from O to each vertex splits the triangle into three smaller triangles, as shown below.

   

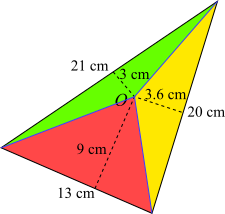
For each smaller triangle, the 'base' and 'height' are shown (the 'bases' are the sides of the original triangle, which are not horizontal). So, using Area $=\dfrac{1}{2}$ base$\times$height, the areas of the smaller triangles can be found:
Red triangle area $\dfrac{1}{2}\times13\times9$
Yellow triangle area $\dfrac{1}{2}\times20\times3.6$
Green triangle area $\dfrac{1}{2}\times21\times3$
So the total area of the triangle is
$\dfrac{13\times9+20\times3.6+21\times3}{2}=\dfrac{117+72+63}{2}=126$cm$^2$


Using trigonometry
The cosine rule can be used to find one of the angles in the triangle, and then the formula $\frac{1}{2}ab\sin{C}$ can be used to find the area.

For example, the angle between the 13 cm side and the 20 cm side can be found using the cosine rule:$$\begin{align}&21^2=13^2+20^2-2\times 13\times20\times\cos{\theta}\\\Rightarrow&441=569-520\cos{\theta}\\\Rightarrow&\cos{\theta}=\frac{569-441}{520}=\frac{128}{5200}=\frac{16}{65}\\\Rightarrow&\theta=75.75^{\text{o}}\end{align}$$

So the area of the triangle is $\frac{1}{2}\times13\times20\times\sin{75.75^{\text{o}}}=126$ cm$^2$.


Using Heron's Forumla
Heron's formula for the area of a triangle with sides $a$, $b$ and $c$ is $\sqrt{s(s-a)(s-b)(s-c)}$, where $s$ is half of the perimeter of the triangle.

For this triangle, $a$, $b$ and $c$ are $13$, $20$ and $21$, and the perimeter is $54$, so $s=27$.

So the area is $$\begin{split}\sqrt{27\times14\times7\times6}&=\sqrt{3^3\times2\times7\times2\times3}\\&=\sqrt{2\times2\times3^2\times3^2\times7\times7}\\&=\sqrt{(2\times3^2\times7)^2}\\&=2\times3^2\times7\\&=126\end{split}$$

So the area is $126$ cm$^2$.