Overlapping Ribbons

Using a parallelogram
In this diagram, the length and perpendicular 'height' of the parallelogram formed by the overlap are marked in red, and a helpful triangle is coloured yellow.

 

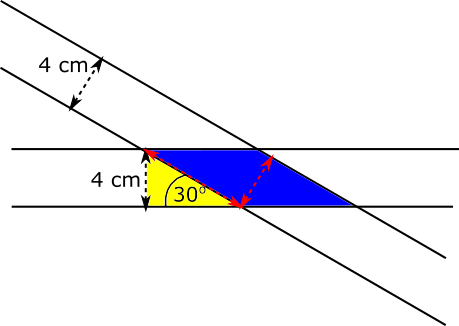
The 'height' of the parallelogram is 4 cm and the length of the parallelogram is equal to the hypotenuse of the yellow triangle. This hypotenuse can be found using trigonometry.

$$\sin{30}=\dfrac{4}{\text{hyp}}\implies\sin{30}\times\text{hyp}=4\implies\text{hyp}=\dfrac{4}{\sin{30}}=8$$

So the length of the parallelogram is 8 cm and its 'height' is 4 cm, so its area is 8$\times$4 = 32 cm$^2$.

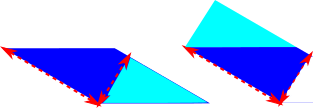
(The formula for the area of a parallelogram can be derived by cutting off and replacing a triangle to transform it into a rectangle as show below)

 

Using areas of triangles
Splitting the shaded area up as shown gives some easier shapes to work with.

 
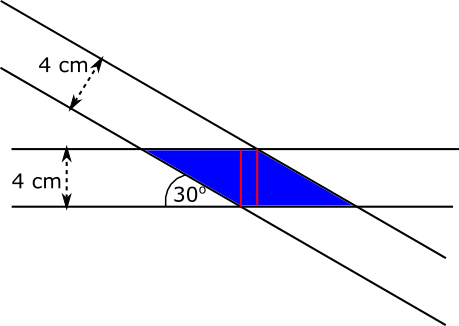
First, the areas of the triangles can be found using $\text{Area}=\dfrac{1}{2}\text{base}\times\text{height}$, where the  length of the base of the triangle can be found using trigonometry.

 

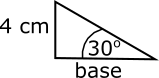
$$\tan{30}=\dfrac{4}{\text{base}}\implies\tan{30}\times\text{base}=4\implies\text{base}=\dfrac{4}{\tan{30}}=4\sqrt{3}$$
So the area of the triangle is $\dfrac{1}{2}\times4\times4\sqrt{3}=8\sqrt{3}$cm$^2$.

To find the area of the thin rectangle, the diagram below is helpful, which shows the rectangle, the lower blue triangle and a yellow right-angled triangle drawn below it.

  
The base of the rectangle and the base of the blue triangle add up to the hypotenuse of the yellow triangle. So finding the hypotenuse of the yellow triangle will enable us to find the base of the rectangle.
$$\sin{30}=\dfrac{4}{\text{hyp}}\implies\sin{30}\times\text{hyp}=4\implies\text{hyp}=\dfrac{4}{\sin{30}}=8$$
So the length of the base of the rectangle is $8-4\sqrt{3}$cm, which means the area of the rectangle is $4\times(8-4\sqrt{3})=32-16\sqrt{3}$cm$^2$.
So the total area of the overlap is 2$\times$area of triangle + area of rectangle, so the area is $2\times8\sqrt{3}+32-16\sqrt{3}=32$cm$^2$.