Skip over navigation
Tilted Tank
Age 11 to 14
ShortChallenge Level 
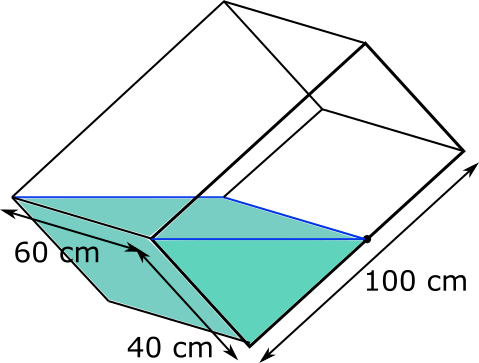
Finding the volume of water in the tank
The water in the tank is in the shape of a triangular prism, as shown, so its volume can be found using length $\times$ area of cross-section.
The cross-section is the triangle on the original diagram, shown again below with the sides labelled.
Because the two sides which are labelled are perpendicular, they can be considered to be the base and height of the triangle, so its area is $\frac{1}{2}\times40\times50=1000$ cm$^2$. So the volume of water in the tank is $60\times1000=60\hspace{1mm}000$ cm$^3$.
When the tank is resting on its base, as shown below, the volume of water in the tank is given by $100\times60h=6000h$ cm$^3$.
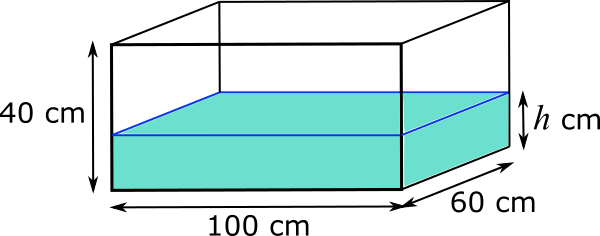
But the volume of water in the tank must also still be $60\hspace{1mm}000$ cm$^3$, so $6000h=60\hspace{1mm}000$. So $h$ must be 10.
So the height of the water is 10 cm.
Using area only
Because the 60 cm edge will stay in contact with the ground as the tank is rotated, the water in the tank will always form a prism whose length is along the 60 cm edge. So since the volume remains unchanged, the area of the cross-section as seen through the 40 cm by 100 cm face will also remain unchanged.
Splitting the face into triangles
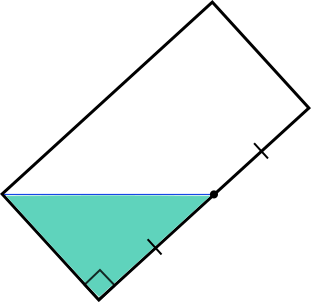
When the tank is tilted, that area is the area of the triangle shown below.
The triangle reaches the midpoint of the longer side, so reflecting in the line of symmetry shown below will create 4 congruent triangles inside the rectangle.
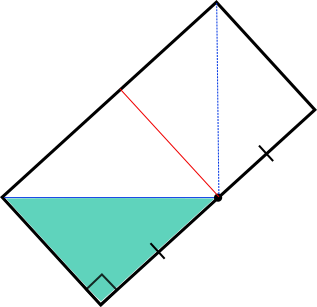
So the tank must be $\frac{1}{4}$ full.
So when it is flat, the height of the water will be $\frac{1}{4}$ of the height of the tank, which is $\frac{1}{4}$ of 40 cm, which is 10 cm.
Finding the area of the water
When the tank is tilted, that area is the area of the triangle shown below.
Because the two sides which are labelled are perpendicular, they can be considered to be the base and height of the triangle, so its area is $\frac{1}{2}\times40\times50=1000$ cm$^2$.
When the tank is flat, that area is the area of the rectangle shown below.
The area of the rectangle is $100\times h$ cm$^2$, so, since this area is still the same as the area of the triangle, $100h=1000$, so $h=10$.
So the height of the water is 10 cm.
The water in the tank is in the shape of a triangular prism, as shown, so its volume can be found using length $\times$ area of cross-section.
The cross-section is the triangle on the original diagram, shown again below with the sides labelled.
Because the two sides which are labelled are perpendicular, they can be considered to be the base and height of the triangle, so its area is $\frac{1}{2}\times40\times50=1000$ cm$^2$. So the volume of water in the tank is $60\times1000=60\hspace{1mm}000$ cm$^3$.
When the tank is resting on its base, as shown below, the volume of water in the tank is given by $100\times60h=6000h$ cm$^3$.
But the volume of water in the tank must also still be $60\hspace{1mm}000$ cm$^3$, so $6000h=60\hspace{1mm}000$. So $h$ must be 10.
So the height of the water is 10 cm.
Using area only
Because the 60 cm edge will stay in contact with the ground as the tank is rotated, the water in the tank will always form a prism whose length is along the 60 cm edge. So since the volume remains unchanged, the area of the cross-section as seen through the 40 cm by 100 cm face will also remain unchanged.
Splitting the face into triangles
When the tank is tilted, that area is the area of the triangle shown below.
The triangle reaches the midpoint of the longer side, so reflecting in the line of symmetry shown below will create 4 congruent triangles inside the rectangle.
So the tank must be $\frac{1}{4}$ full.
So when it is flat, the height of the water will be $\frac{1}{4}$ of the height of the tank, which is $\frac{1}{4}$ of 40 cm, which is 10 cm.
Finding the area of the water
When the tank is tilted, that area is the area of the triangle shown below.
Because the two sides which are labelled are perpendicular, they can be considered to be the base and height of the triangle, so its area is $\frac{1}{2}\times40\times50=1000$ cm$^2$.
When the tank is flat, that area is the area of the rectangle shown below.
The area of the rectangle is $100\times h$ cm$^2$, so, since this area is still the same as the area of the triangle, $100h=1000$, so $h=10$.
So the height of the water is 10 cm.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Hallway Borders
What are the possible dimensions of a rectangular hallway if the number of tiles around the perimeter is exactly half the total number of tiles?
