Skip over navigation
Answer: 10 tiles by 17 tiles
Finding an expression for the change in the number of tiles
Original patio:

Shorten one side by 3 tiles:
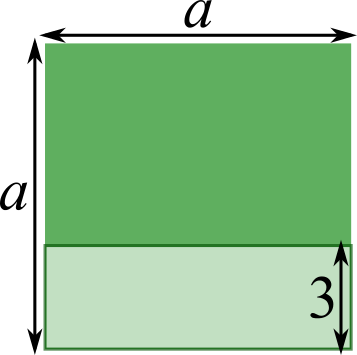 Removed 3$a$ tiles
Removed 3$a$ tiles
Other side 4 tiles longer:
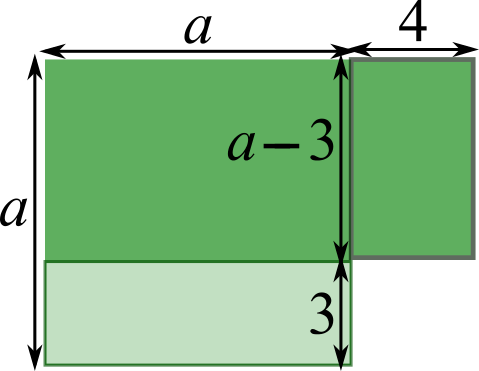 Added 4$(a-$3$)$ tiles.
Added 4$(a-$3$)$ tiles.
Needed 1 extra tile to make this change, so 4$(a-$3$)$ = 3$a$ + 1, so 4$a-$12 = 3$a$ + 1, so $a-$12 = 1, so $a$ = 13.
13 tiles by 13 tiles square $\Rightarrow$ 10 tiles by 17 tiles rectangle.
Using quadratic expressions for the total area before and after
Before: After:

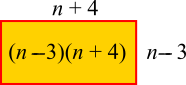
The new arrangement uses one extra tile, so $$\begin{align}n^2+1&=(n-3)(n+4)\\
n^2+1&=n^2+4n-3n-12\\
n^2+1&=n^2+n-12\\
1&=n-12\\
13&=n\end{align}$$
So Kevin had a $13$ tiles by $13$ tiles square, which means that he made a $10$ tiles by $17$ tiles rectangle.
Trying out numbers
The patio used to be a square, so we can test some square numbers to see whether they work.
If the patio started as a 10 tiles by 10 tiles square, then Kevin would have had 100 tiles.
Making one side 3 tiles shorter and the other side 4 tiles longer would have given him a 7 by 14 rectangle.
7$\times$14 = 98, so Kevin would have had 2 spare tiles if he had started off with a 10 by 10 square. But Kevin needed 1 extra tile, so that can't be right.
If the patio started as a 9 tiles by 9 tiles square, then Kevin would have had 81 tiles.
Making one side 3 tiles shorter and the other side 4 tiles longer would have given him a 6 by 13 rectangle.
6$\times$13 = 78, so Kevin would have had 3 spare tiles if he had started off with a 9 by 9 square. That is worse than the 10 by 10 square, because the 10 by 10 square would only have given Kevin 2 spare tiles. So Kevin's patio must have started as a square that was larger than 10 tiles by 10 tiles.
If the patio started as a 12 tiles by 12 tiles square, then Kevin would have had 144 tiles.
Making one side 3 tiles shorter and the other side 4 tiles longer would have given him a 9 by 16 rectangle.
9$\times$16 = 144, so Kevin would have had exactly the right number of tiles if he started off with a 12 by 12 square and wouldn't have needed to buy 1 extra tile.
If the patio started as a 13 tiles by 13 tiles square, then Kevin would have had 169 tiles.
Making one side 3 tiles shorter and the other side 4 tiles longer would give him a 10 by 17 rectangle.
10$\times$17 = 170, so Kevin would need 1 extra tile to make the rectangle - which is right!
So he must have made a 10 tiles by 17 tiles rectangle.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Square to a Rectangle
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Answer: 10 tiles by 17 tiles
Finding an expression for the change in the number of tiles
Original patio:

Shorten one side by 3 tiles:
 Removed 3$a$ tiles
Removed 3$a$ tilesOther side 4 tiles longer:
 Added 4$(a-$3$)$ tiles.
Added 4$(a-$3$)$ tiles.Needed 1 extra tile to make this change, so 4$(a-$3$)$ = 3$a$ + 1, so 4$a-$12 = 3$a$ + 1, so $a-$12 = 1, so $a$ = 13.
13 tiles by 13 tiles square $\Rightarrow$ 10 tiles by 17 tiles rectangle.
Using quadratic expressions for the total area before and after
Before: After:

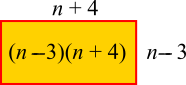
The new arrangement uses one extra tile, so $$\begin{align}n^2+1&=(n-3)(n+4)\\
n^2+1&=n^2+4n-3n-12\\
n^2+1&=n^2+n-12\\
1&=n-12\\
13&=n\end{align}$$
So Kevin had a $13$ tiles by $13$ tiles square, which means that he made a $10$ tiles by $17$ tiles rectangle.
Trying out numbers
The patio used to be a square, so we can test some square numbers to see whether they work.
If the patio started as a 10 tiles by 10 tiles square, then Kevin would have had 100 tiles.
Making one side 3 tiles shorter and the other side 4 tiles longer would have given him a 7 by 14 rectangle.
7$\times$14 = 98, so Kevin would have had 2 spare tiles if he had started off with a 10 by 10 square. But Kevin needed 1 extra tile, so that can't be right.
If the patio started as a 9 tiles by 9 tiles square, then Kevin would have had 81 tiles.
Making one side 3 tiles shorter and the other side 4 tiles longer would have given him a 6 by 13 rectangle.
6$\times$13 = 78, so Kevin would have had 3 spare tiles if he had started off with a 9 by 9 square. That is worse than the 10 by 10 square, because the 10 by 10 square would only have given Kevin 2 spare tiles. So Kevin's patio must have started as a square that was larger than 10 tiles by 10 tiles.
If the patio started as a 12 tiles by 12 tiles square, then Kevin would have had 144 tiles.
Making one side 3 tiles shorter and the other side 4 tiles longer would have given him a 9 by 16 rectangle.
9$\times$16 = 144, so Kevin would have had exactly the right number of tiles if he started off with a 12 by 12 square and wouldn't have needed to buy 1 extra tile.
If the patio started as a 13 tiles by 13 tiles square, then Kevin would have had 169 tiles.
Making one side 3 tiles shorter and the other side 4 tiles longer would give him a 10 by 17 rectangle.
10$\times$17 = 170, so Kevin would need 1 extra tile to make the rectangle - which is right!
So he must have made a 10 tiles by 17 tiles rectangle.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Picture Story
Can you see how this picture illustrates the formula for the sum of the first six cube numbers?
There and Back
Brian swims at twice the speed that a river is flowing, downstream from one moored boat to another and back again, taking 12 minutes altogether. How long would it have taken him in still water?
Doesn't Add Up
In this problem we are faced with an apparently easy area problem, but it has gone horribly wrong! What happened?

