Graph Area

Plotting the graph using a table of values
If we plot the graph first, then we will be able to see the shape whose area we are looking for.

We can use a table of values to plot the graph, and we are interested in $x$ values between $3$ and $7$, so going from $2$ to $8$ will help us see the whole shape.

If $x=2$, then $y=2\times2-6=4-6=-2$. The rest of the values can be found in the same way.

$x$	$2$	$3$	$4$	$5$	$6$	$7$	$8$
$y$	$-2$	$0$	$2$	$4$	$6$	$8$	$10$

The graph looks like this:



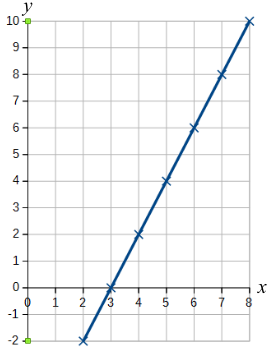
We need to find the area between $x=3$ and $x=7$, which is coloured green below.

 
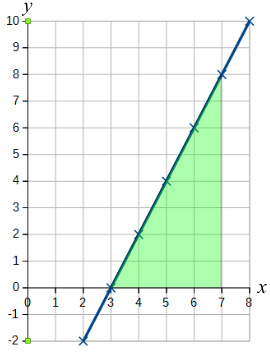
The shape is a right-angled triangle, and its base is $4$ units and its height is $8$ units. So its area is $\frac{1}{2}\times4\times8=16$ square units.


Sketching the graph using relevant points
From the equation $y=2x-6$, we know that the graph will be a straight line.

Since we are interested in the area between $x=3$ and $x=7$, we could check where the graph is at those two points.

When $x=3$, $y=2\times3-6=6-6=0$.
When $x=7$, $y=2\times7-6=14-6=8$.

So $(3,0)$ and $(7,8)$ lie on the graph.



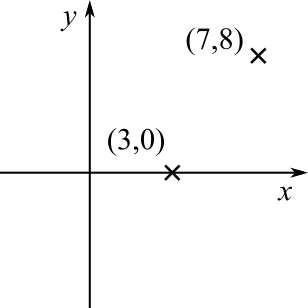
So the graph must be the straight line through those points, and the area required is the green area, as shown below.



The shape is a right-angled triangle, and its base is $4$ units and its height is $8$ units. So its area is $\frac{1}{2}\times4\times8=16$ square units.