Skip over navigation
Answer: you have a better chance of winning the letters game
Using a tree diagram beginning by checking for duplicated numbers/letters
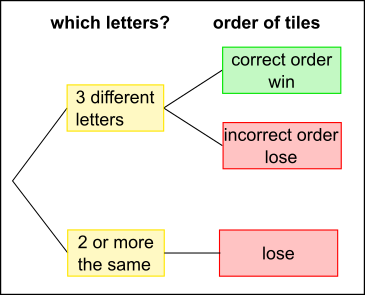
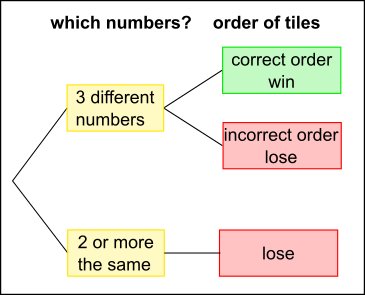
Given 3 numbers or 3 letters which are all different, the probability that they are in order is the same.
Call this probability $\text p$.
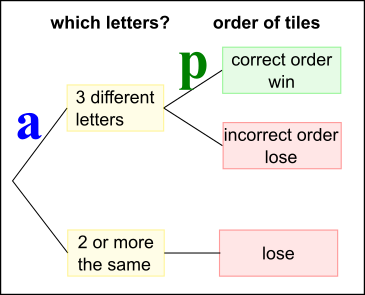
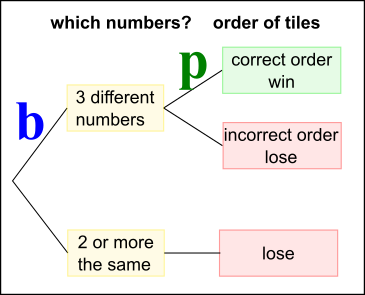
Which is greater out of $\text a$ and $\text b$?
More likely to get repeats using 10 tiles than 26 tiles, so more likely to get 3 different with 26 tiles (letters).
So $\text a \gt \text b$ - you are more likely to win the letters game.
Creating all of the winning combinations
Probability of winning numbers game is $$\frac{\text{number of number combinations in the right order}}{\text{total number of possible number combinations}}$$
Total number of possible number combinations is $10\times10\times10 = 1000$
Number of winning combinations:
Total number of options: $$1\times8 + 2\times 7 +3\times6+4\times5+5\times4+6\times3+7\times2+8\times1\\
= (8+14+18+20)\times 2\\
=120$$
$\therefore$ probability of winning numbers game is $\dfrac{120}{1000}$
Total number of possible letter combinations is $26\times26\times26$
Total number of options will be: $$(1\times24 + 2\times23 + 3\times22 + ... + 12\times13)\times2\\
= (24+46+66+84+100+114+126+136+144+150+154+156)\times2\\
= 2600$$
$\therefore$ probability of winning letters game is $\dfrac{2600}{26\times26\times26}$
Which is bigger?
$\dfrac{120}{1000}=\dfrac{12}{100}=\dfrac{24}{200}$
$\dfrac{2600}{26\times26\times26} = \dfrac {100}{26\times26} = \dfrac{25}{13\times13} = \dfrac{25}{169}>\dfrac{24}{200}$
More likely to win the letters game
Counting winning possibilities by considering combinations
Probability of winning numbers game is $$\frac{\text{number of number combinations in the right order}}{\text{total number of possible number combinations}}$$
Total number of possible number combinations is $10\times10\times10 = 1000$
Now we need the number of number combinations in the right order.
Must have 3 different numbers, which then can be put in order:
Tile A: $10$ options
Tile B: $9$ options
Tile C: $8$ options
So $10\times9\times8 = 720$ ways get three different numbers.
But some are counted twice: $4, 6, 3$ and $6, 3, 4$ and so on - but both score a point as $3, 4, 6.$
How many times is $3, 4, 6$ counted?
Tile A: $3$ options ($3, 4$ or $6$)
Tile B: $2$ options
Tile C: $1$ option
$3\times2\times1 = 6$ times.
So there are $720\div6 = 120$ winning combinations.
Probability of winning numbers game is $\dfrac{120}{1000}=\dfrac{3}{25}$
Similarly, for letters:
$26\times26\times26$ possible combinations.
$(26\times25\times24)\div(3\times2\times1) = 26\times25\times4$ winning combinations.
Probability of winning letters game is $\dfrac{26\times25\times4}{26\times26\times26}\gt \dfrac3{25}$



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Numbers or Letters?
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Answer: you have a better chance of winning the letters game
Using a tree diagram beginning by checking for duplicated numbers/letters


Given 3 numbers or 3 letters which are all different, the probability that they are in order is the same.
Call this probability $\text p$.


Which is greater out of $\text a$ and $\text b$?
More likely to get repeats using 10 tiles than 26 tiles, so more likely to get 3 different with 26 tiles (letters).
So $\text a \gt \text b$ - you are more likely to win the letters game.
Creating all of the winning combinations
Probability of winning numbers game is $$\frac{\text{number of number combinations in the right order}}{\text{total number of possible number combinations}}$$
Total number of possible number combinations is $10\times10\times10 = 1000$
Number of winning combinations:
| First tile | Second tile | Third tile | Number of options |
| 0 | 1 | 2, 3, 4, ..., 9 | 8 |
| 2 | 3, 4, ..., 9 | 7 | |
| 3 | 4, ..., 9 | 6 | |
| 4 | 5 | ||
| 5 | 4 | ||
| 6 | 3 | ||
| 7 | 8, 9 | 2 | |
| 8 | 9 | 1 | |
| 1 | 2 | 3, 4, 5, ..., 9 | 7 |
| 3 | 6 | ||
| 4 | 5 | ||
| ... | ... | ||
| 8 | 9 | 1 | |
| 2 | 3 | 4, 5, ..., 9 | 6 |
| 4 | 5 | ||
| 5 | 4 | ||
| ... | ... | ||
| 8 | 1 | ||
| 3 | 5 + 4 + 3 + 2 + 1 | ||
| 4 | 4 + 3 + 2 + 1 | ||
| 5 | 3 + 2 + 1 | ||
| 6 | 2 + 1 | ||
| 7 | 8 | 9 | 1 |
Total number of options: $$1\times8 + 2\times 7 +3\times6+4\times5+5\times4+6\times3+7\times2+8\times1\\
= (8+14+18+20)\times 2\\
=120$$
$\therefore$ probability of winning numbers game is $\dfrac{120}{1000}$
Total number of possible letter combinations is $26\times26\times26$
Total number of options will be: $$(1\times24 + 2\times23 + 3\times22 + ... + 12\times13)\times2\\
= (24+46+66+84+100+114+126+136+144+150+154+156)\times2\\
= 2600$$
$\therefore$ probability of winning letters game is $\dfrac{2600}{26\times26\times26}$
Which is bigger?
$\dfrac{120}{1000}=\dfrac{12}{100}=\dfrac{24}{200}$
$\dfrac{2600}{26\times26\times26} = \dfrac {100}{26\times26} = \dfrac{25}{13\times13} = \dfrac{25}{169}>\dfrac{24}{200}$
More likely to win the letters game
Counting winning possibilities by considering combinations
Probability of winning numbers game is $$\frac{\text{number of number combinations in the right order}}{\text{total number of possible number combinations}}$$
Total number of possible number combinations is $10\times10\times10 = 1000$
Now we need the number of number combinations in the right order.
Must have 3 different numbers, which then can be put in order:
Tile A: $10$ options
Tile B: $9$ options
Tile C: $8$ options
So $10\times9\times8 = 720$ ways get three different numbers.
But some are counted twice: $4, 6, 3$ and $6, 3, 4$ and so on - but both score a point as $3, 4, 6.$
How many times is $3, 4, 6$ counted?
Tile A: $3$ options ($3, 4$ or $6$)
Tile B: $2$ options
Tile C: $1$ option
$3\times2\times1 = 6$ times.
So there are $720\div6 = 120$ winning combinations.
Probability of winning numbers game is $\dfrac{120}{1000}=\dfrac{3}{25}$
Similarly, for letters:
$26\times26\times26$ possible combinations.
$(26\times25\times24)\div(3\times2\times1) = 26\times25\times4$ winning combinations.
Probability of winning letters game is $\dfrac{26\times25\times4}{26\times26\times26}\gt \dfrac3{25}$
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Gambling at Monte Carlo
A man went to Monte Carlo to try and make his fortune. Is his strategy a winning one?
Marbles and Bags
Two bags contain different numbers of red and blue marbles. A marble is removed from one of the bags. The marble is blue. What is the probability that it was removed from bag A?
Coin Tossing Games
You and I play a game involving successive throws of a fair coin. Suppose I pick HH and you pick TH. The coin is thrown repeatedly until we see either two heads in a row (I win) or a tail followed by a head (you win). What is the probability that you win?

