Skip over navigation
Begin by counting how many dominoes there are in the set:
Each number appears once with every other number, and once with itself, so starting with the blanks, we can count the number of dominoes in the set.
There are 7 dominoes which have at least one end blank, because a blank appears with all of the different numbers.
There are 6 more dominoes which have at least one 1, because 1 appears with all of the different numbers, but we have already counted the blank.
Continuing in this way, there are 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28 dominoes in the set.
Next, there are several methods:
Considering probabilities using a tree diagram
A tree diagram is not necessary for this approach but it can be helpful.
Imagine taking the two dominoes one by one. The probability of the second domino matching the first will be different if the first is a double, so the tree diagram looks like this.
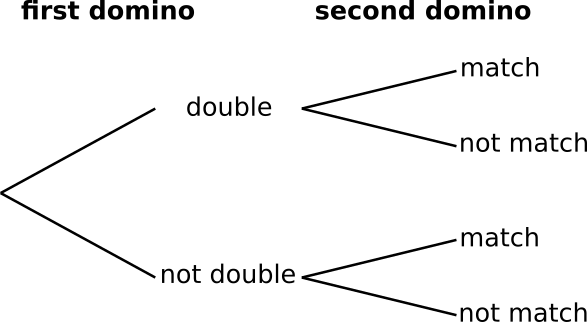
There are 7 doubles in the set, so the probabilities on the first branches can be filled in, as shown below.
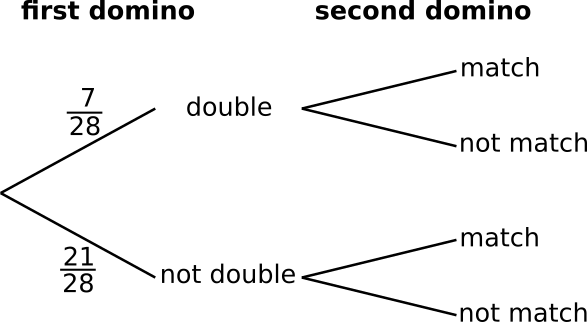
If a double was chosen first - for example, 4|4 - then only the dominoes with a 4 would match. The 4 appears with all of the other numbers, so there are 6 more 4s left. So 6 of the 27 remaining dominoes would match.
If the domino chosen first was not a double, then the second domino could match either end of the first domino. So, for example, if the first domino was 3|4, then any of the 6 other 3s or the 6 other 4s would match - so in total, 12 of the other dominoes would match.
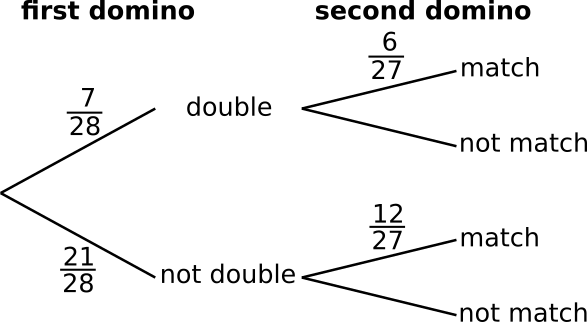
So the probability that the second domino matches the first domino is $\frac{7}{28}\times\frac{6}{27}+\frac{21}{28}\times\frac{12}{27}$. Beginning by simplifying the fractions, that is equal to $\frac{1}{4}\times\frac{2}{9}+\frac{3}{4}\times\frac{4}{9}=\frac{1}{18}+\frac{6}{18}=\frac{7}{18}$.
Counting the matching pairs
When selecting two dominoes from the set, there are 28 choices for the 'first' domino and 27 choices for the 'second' domino, which gives 28$\times$27 pairs. However, this counts every pair twice, because 3|5 as the first domino and 4|1 as the second domino is the same pair as 4|1 first and 3|5 second. So in fact there are 28$\times$27$\div$2 = 378 possible pairs.
To count the matching pairs, it is easier to count the matching pairs where one of the dominoes is a double, and then the matching pairs where neither of the dominoes is a double (two doubles can never match).
If one of the dominoes is a double, then it is one of 7 doubles. The number which is on this domino also appears with all of the other numbers, so it appears 6 more times. So there are 7$\times$6 = 42 matching pairs where one of the dominoes is a double.
There are 28$-$7 = 21 dominoes which are not doubles. Each of these matches 10 other non-doubles - for example, for 3|4, then any of the other 3s or the other 4s would match. There are 5 other 3s and 5 other 4s (not counting the double 3 or the double 4), so in total, 10 of the other non-doubles would match. That almost gives 21$\times$10 matching pairs where neither of the dominoes is a double, but the pairs are all counted twice, since 3|4 and 3|6 is the same as 3|6 and 3|4. So there are 21$\times$10$\div$2 = 105 matching pairs where neither of the dominoes is a double.
So in total, there are 42 + 105 = 147 matching pairs of dominoes, out of a possible 378 pairs. So the probability of choosing a matching pair of dominoes is $\frac{147}{378}$, which simplifies to $\frac{7}{18}$.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Domino Match
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Begin by counting how many dominoes there are in the set:
Each number appears once with every other number, and once with itself, so starting with the blanks, we can count the number of dominoes in the set.
There are 7 dominoes which have at least one end blank, because a blank appears with all of the different numbers.
There are 6 more dominoes which have at least one 1, because 1 appears with all of the different numbers, but we have already counted the blank.
Continuing in this way, there are 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28 dominoes in the set.
Next, there are several methods:
Considering probabilities using a tree diagram
A tree diagram is not necessary for this approach but it can be helpful.
Imagine taking the two dominoes one by one. The probability of the second domino matching the first will be different if the first is a double, so the tree diagram looks like this.

There are 7 doubles in the set, so the probabilities on the first branches can be filled in, as shown below.

If a double was chosen first - for example, 4|4 - then only the dominoes with a 4 would match. The 4 appears with all of the other numbers, so there are 6 more 4s left. So 6 of the 27 remaining dominoes would match.
If the domino chosen first was not a double, then the second domino could match either end of the first domino. So, for example, if the first domino was 3|4, then any of the 6 other 3s or the 6 other 4s would match - so in total, 12 of the other dominoes would match.

So the probability that the second domino matches the first domino is $\frac{7}{28}\times\frac{6}{27}+\frac{21}{28}\times\frac{12}{27}$. Beginning by simplifying the fractions, that is equal to $\frac{1}{4}\times\frac{2}{9}+\frac{3}{4}\times\frac{4}{9}=\frac{1}{18}+\frac{6}{18}=\frac{7}{18}$.
Counting the matching pairs
When selecting two dominoes from the set, there are 28 choices for the 'first' domino and 27 choices for the 'second' domino, which gives 28$\times$27 pairs. However, this counts every pair twice, because 3|5 as the first domino and 4|1 as the second domino is the same pair as 4|1 first and 3|5 second. So in fact there are 28$\times$27$\div$2 = 378 possible pairs.
To count the matching pairs, it is easier to count the matching pairs where one of the dominoes is a double, and then the matching pairs where neither of the dominoes is a double (two doubles can never match).
If one of the dominoes is a double, then it is one of 7 doubles. The number which is on this domino also appears with all of the other numbers, so it appears 6 more times. So there are 7$\times$6 = 42 matching pairs where one of the dominoes is a double.
There are 28$-$7 = 21 dominoes which are not doubles. Each of these matches 10 other non-doubles - for example, for 3|4, then any of the other 3s or the other 4s would match. There are 5 other 3s and 5 other 4s (not counting the double 3 or the double 4), so in total, 10 of the other non-doubles would match. That almost gives 21$\times$10 matching pairs where neither of the dominoes is a double, but the pairs are all counted twice, since 3|4 and 3|6 is the same as 3|6 and 3|4. So there are 21$\times$10$\div$2 = 105 matching pairs where neither of the dominoes is a double.
So in total, there are 42 + 105 = 147 matching pairs of dominoes, out of a possible 378 pairs. So the probability of choosing a matching pair of dominoes is $\frac{147}{378}$, which simplifies to $\frac{7}{18}$.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Dominoes
Everthing you have always wanted to do with dominoes! Some of these games are good for practising your mental calculation skills, and some are good for your reasoning skills.
Domino Magic Rectangle
An ordinary set of dominoes can be laid out as a 7 by 4 magic rectangle in which all the spots in all the columns add to 24, while those in the rows add to 42. Try it! Now try the magic square...

