Skip over navigation
Labelling horizontal and vertical distances using letters
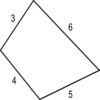
Drawing on vertical and horizontal distances from the well to the corners and labelling them $a,b,c$ and $d$ gives the image below.
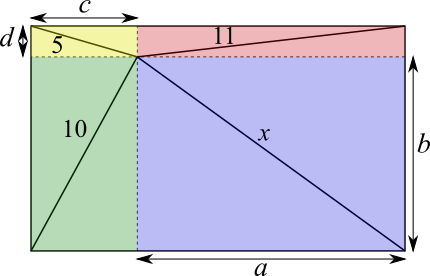
From the blue rectangle, $a^2+b^2=x^2$.
From the green rectangle, $b^2+c^2=100$.
From the red rectangle, $a^2+d^2=121$.
From the yellow rectangle, $c^2+d^2=25$.
Adding the equations given by the green and red rectangles gives $$\begin{align}b^2+c^2+a^2+d^2=&100+121\\ \Rightarrow \left(a^2+b^2\right)+\left(c^2+d^2\right)=&221\end{align}$$ And now substituting $a^2+b^2=x^2$ and $c^2+d^2=25$ gives $$\begin{align}&x^2+25=221\\ \Rightarrow&x^2=196\\ \Rightarrow &x=14\end{align}$$
Using a diagram
In the diagram below, the courtyard has been split into 4 rectangles whose corners are at the well. The squares drawn on are for the diagrammatic representation of Pythagoras' theorem, so that the area of shaded square A added to the area of shaded square B is equal to $x^2$, because $x$ is the hypotenuse of the triangle in the blue rectangle.
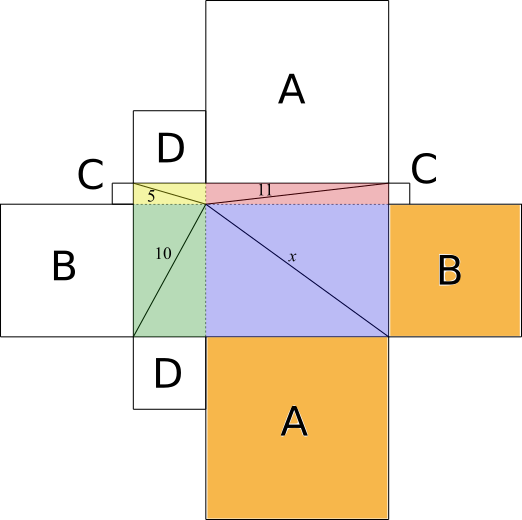
Without using the blue rectangle, how else can we get A+B?
The square of the hypotenuse in the red rectangle is A+C, and the square of the green rectangle is B+D. Adding these together gives A+B+C+D, which is too much by C+D. But the square of the hypotenuse in the yellow rectangle is C+D.
So A+B=11$^2$+10$^2-$5$^2$=196.
So $x^2$ = 196, so $x$ = 14.
Using vectors and the scalar product
In the diagram below, the vectors from the well to the four corners of the rectangle are labelled $\bf{a,b,c}$ and $\bf{x}$.
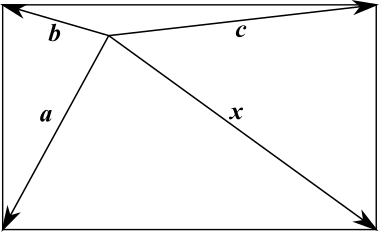
From the diagram below, it can be seen that the vector $\bf{x}$ is equal to $\bf{a}+\bf{c}-\bf{b}$, and that the sides of the rectangle can be written as $\bf{b}-\bf{a}$ and $\bf{c}-\bf{b}$.
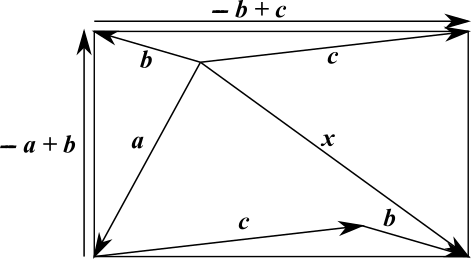
The sides of the rectangle are perpendicular, so $$\begin{align}\left(\bf{b-a}\right).\left(\bf{c-b}\right)&=0\\\Rightarrow\bf{b.c-b.b-a.c+a.b}&=0\\\Rightarrow\bf{b.c-b.b+a.b}=\bf{a.c}\end{align}$$ And we are looking for $\sqrt{\bf{x.x}}$, where $$\begin{split}\bf{x.x}&=\left(\bf{a+c-b}\right).\left(\bf{a+c-b}\right)\\&=\bf{a.a+b.b+c.c+}2\bf{a.c}-2\bf{a.b}-2\bf{c.b}\end{split}$$So, substituting $\bf{b.c-b.b+a.b}=\bf{a.c}$, $$\begin{split}\bf{x.x}&=\bf{a.a+b.b+c.c+}2\left(\bf{b.c-b.b+a.b}\right)-2\bf{a.b}-2\bf{c.b}\\&=\bf{a.a+b.b+c.c-}2\bf{b.b}\\&=\bf{a.a+c.c-b.b}\end{split}$$
But $\bf{a.a}$$=10^2=100,$ $\bf{b.b}$$=5^2=25,$ $\bf{c.c}$$=11^2=121$, so $\bf{x.x}$$=100+121-25=196=14^2$.
So the remaining distance is $14$.
Distance to the Corner
Age 14 to 16
ShortChallenge Level 
Labelling horizontal and vertical distances using letters
Drawing on vertical and horizontal distances from the well to the corners and labelling them $a,b,c$ and $d$ gives the image below.
From the blue rectangle, $a^2+b^2=x^2$.
From the green rectangle, $b^2+c^2=100$.
From the red rectangle, $a^2+d^2=121$.
From the yellow rectangle, $c^2+d^2=25$.
Adding the equations given by the green and red rectangles gives $$\begin{align}b^2+c^2+a^2+d^2=&100+121\\ \Rightarrow \left(a^2+b^2\right)+\left(c^2+d^2\right)=&221\end{align}$$ And now substituting $a^2+b^2=x^2$ and $c^2+d^2=25$ gives $$\begin{align}&x^2+25=221\\ \Rightarrow&x^2=196\\ \Rightarrow &x=14\end{align}$$
Using a diagram
In the diagram below, the courtyard has been split into 4 rectangles whose corners are at the well. The squares drawn on are for the diagrammatic representation of Pythagoras' theorem, so that the area of shaded square A added to the area of shaded square B is equal to $x^2$, because $x$ is the hypotenuse of the triangle in the blue rectangle.
Without using the blue rectangle, how else can we get A+B?
The square of the hypotenuse in the red rectangle is A+C, and the square of the green rectangle is B+D. Adding these together gives A+B+C+D, which is too much by C+D. But the square of the hypotenuse in the yellow rectangle is C+D.
So A+B=11$^2$+10$^2-$5$^2$=196.
So $x^2$ = 196, so $x$ = 14.
Using vectors and the scalar product
In the diagram below, the vectors from the well to the four corners of the rectangle are labelled $\bf{a,b,c}$ and $\bf{x}$.
From the diagram below, it can be seen that the vector $\bf{x}$ is equal to $\bf{a}+\bf{c}-\bf{b}$, and that the sides of the rectangle can be written as $\bf{b}-\bf{a}$ and $\bf{c}-\bf{b}$.
The sides of the rectangle are perpendicular, so $$\begin{align}\left(\bf{b-a}\right).\left(\bf{c-b}\right)&=0\\\Rightarrow\bf{b.c-b.b-a.c+a.b}&=0\\\Rightarrow\bf{b.c-b.b+a.b}=\bf{a.c}\end{align}$$ And we are looking for $\sqrt{\bf{x.x}}$, where $$\begin{split}\bf{x.x}&=\left(\bf{a+c-b}\right).\left(\bf{a+c-b}\right)\\&=\bf{a.a+b.b+c.c+}2\bf{a.c}-2\bf{a.b}-2\bf{c.b}\end{split}$$So, substituting $\bf{b.c-b.b+a.b}=\bf{a.c}$, $$\begin{split}\bf{x.x}&=\bf{a.a+b.b+c.c+}2\left(\bf{b.c-b.b+a.b}\right)-2\bf{a.b}-2\bf{c.b}\\&=\bf{a.a+b.b+c.c-}2\bf{b.b}\\&=\bf{a.a+c.c-b.b}\end{split}$$
But $\bf{a.a}$$=10^2=100,$ $\bf{b.b}$$=5^2=25,$ $\bf{c.c}$$=11^2=121$, so $\bf{x.x}$$=100+121-25=196=14^2$.
So the remaining distance is $14$.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
Bendy Quad
Four rods are hinged at their ends to form a convex quadrilateral. Investigate the different shapes that the quadrilateral can take. Be patient this problem may be slow to load.