Skip over navigation
Triangular Intersection
Age 14 to 16
ShortChallenge Level 
Every quadrilateral is made up of 4 lines, and extending these lines on beyond the vertices of the quadrilaterals is helpful to explain why there cannot be more than 8 intersection points.
Starting from one of its vertices, a triangle can be drawn anywhere without taking the pencil off the paper, but must finish where it started.
This means that every line crossed must be crossed back again - so each of the 4 lines which make up the quadrilateral must be crossed an even number of times.
The triangle only has 3 sides, so it cannot cross any of the lines which make up the quadrilateral more than 3 times. So each of the lines which make up the quadrilateral must be crossed 0 or 2 times.
If each side is crossed 2 times, that makes a total of 8 intersection points - so there can never be more than 8 intersection points.
An example of a triangle and a quadrilateral with 8 intersection points is shown below.
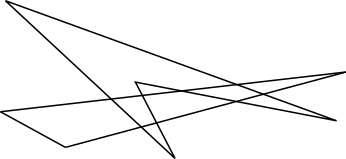
Starting from one of its vertices, a triangle can be drawn anywhere without taking the pencil off the paper, but must finish where it started.
This means that every line crossed must be crossed back again - so each of the 4 lines which make up the quadrilateral must be crossed an even number of times.
The triangle only has 3 sides, so it cannot cross any of the lines which make up the quadrilateral more than 3 times. So each of the lines which make up the quadrilateral must be crossed 0 or 2 times.
If each side is crossed 2 times, that makes a total of 8 intersection points - so there can never be more than 8 intersection points.
An example of a triangle and a quadrilateral with 8 intersection points is shown below.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Doodles
Draw a 'doodle' - a closed intersecting curve drawn without taking pencil from paper. What can you prove about the intersections?
Russian Cubes
I want some cubes painted with three blue faces and three red faces. How many different cubes can be painted like that?
Polycircles
Show that for any triangle it is always possible to construct 3 touching circles with centres at the vertices. Is it possible to construct touching circles centred at the vertices of any polygon?