Skip over navigation
Were were only half way through gathering solutions, when these pupils, sent in good solutions. I ask the teacher to contact Nrich to say which school they all come from,?
These came in from St Mary's C of E Primary school Chipping Norton
Joanna and Arthur
We drew a picture to help us and it looked like a wonky staircase. When we did it the first time, we used 18(1/2) 12(1/3) 9(1/4) and 6(1/6). We added them together and we got 1 1/4. When we compared it to the light blue; we got 3 1/4, so the second answer was 2 more than the first.
Cadence
When I compared the blue results with the black results I found out that the answers for blue were three times the answers for black. This due to blue being three times smaller than the black meaning that every fraction that only went into black only once would go into the blue three times more. This is the same for brown. Because brown is half the size of black every fraction that went into black once would go into brown twice. Because green is one quarter the size of black any fraction that went into black once would into green four times. And so on. And that is the answer to another Nrich puzzle. Thank you for reading.
Kaya
I found that, when Incompared my answers for the blue and black strips, they were fairly similar. The answer for he blue strip was three times bigger than the answer for the black strip. This was due to the blue strip being three times smaller, so it went into one more times. For example, brown would be two times bigger than black, due to it being two times smaller. This puzzle was quite challenging at first, but soon became easy when I found out this rule. I really enjoyed taking part in this challenge, and Thank You for reading.

Maisie and Rebecca
We found that with our solution (2 quarters, a half and a twelfth) that with the blue bar it made 3 and 1 twelfth and with the black it made 1 and a twelfth.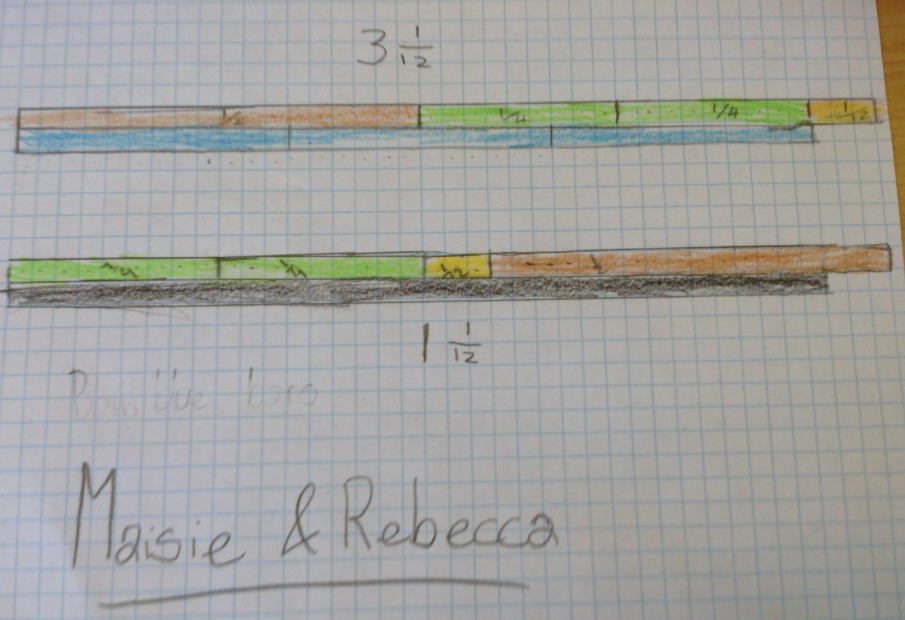

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Fraction Lengths
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Were were only half way through gathering solutions, when these pupils, sent in good solutions. I ask the teacher to contact Nrich to say which school they all come from,?
Cordelia, Eva-Lilly and Jess, Ellis, Kian, Reg and Rohan, Jaiden and Krrish, Reina and Sienna, Hannah and Ruby, Kush and Tom
Please make contact primary.nrich@maths.org
These came in from St Mary's C of E Primary school Chipping Norton
Joanna and Arthur
We drew a picture to help us and it looked like a wonky staircase. When we did it the first time, we used 18(1/2) 12(1/3) 9(1/4) and 6(1/6). We added them together and we got 1 1/4. When we compared it to the light blue; we got 3 1/4, so the second answer was 2 more than the first.
Cadence
When I compared the blue results with the black results I found out that the answers for blue were three times the answers for black. This due to blue being three times smaller than the black meaning that every fraction that only went into black only once would go into the blue three times more. This is the same for brown. Because brown is half the size of black every fraction that went into black once would go into brown twice. Because green is one quarter the size of black any fraction that went into black once would into green four times. And so on. And that is the answer to another Nrich puzzle. Thank you for reading.
Kaya
I found that, when Incompared my answers for the blue and black strips, they were fairly similar. The answer for he blue strip was three times bigger than the answer for the black strip. This was due to the blue strip being three times smaller, so it went into one more times. For example, brown would be two times bigger than black, due to it being two times smaller. This puzzle was quite challenging at first, but soon became easy when I found out this rule. I really enjoyed taking part in this challenge, and Thank You for reading.

Maisie and Rebecca
We found that with our solution (2 quarters, a half and a twelfth) that with the blue bar it made 3 and 1 twelfth and with the black it made 1 and a twelfth.

From Ryanne at Westridge School in Pasadena USA we had this exaplanation.
When I was looking at the the black stnip I noticed that it was equal to one whole and that it was 36 squares long. Then I looked at the red block or number 4, I thought to myself that 4 is a multiple of 36 because it goes into it 9 times, you could put four red blocks which would be equal to 36, because 4 times 9 equals 36. Another one I found was that the brown stnip is worth 18, if' you know what half of 36 is then you will know that 18 is half, therefore if 18 is half and the brown stn'p is worth 18 then two of those stnips ought to be equal to 36. you can also use two greens, because 9 + 9 = 18 and like I said before 18 is half of the black strip, so two greens is equal to 18 plus 3 more pinks which equals 18 you would get 18 + 18 = 36. Last but not least, 2 twelves, because if 1 twelve fits half the black stnip then 2 is equal to 36.
Now we are using 3 light blue strips for the whole. It says to choose four stnips, so I will chose yellow, green, pink, and brown. So now when I compare them to the three light blue stnips it is not equal to the three light blue strips it is less. So now I will be trying yellow, green, light blue, and brown. My result is that this time it still not equal to the three light blue stnips infact it is going over by 5 squares. This time I will use brown. "9'" blue, green, pink the outcome is that I still can 't get them to equal the three light blue strips.
That's a really good explanation. Thank you for sharing where you got to with the second part. Can anyone help Ryanne?
Thank you for all these submitted solutions keep looking at other Nrich activities.
When I was looking at the the black stnip I noticed that it was equal to one whole and that it was 36 squares long. Then I looked at the red block or number 4, I thought to myself that 4 is a multiple of 36 because it goes into it 9 times, you could put four red blocks which would be equal to 36, because 4 times 9 equals 36. Another one I found was that the brown stnip is worth 18, if' you know what half of 36 is then you will know that 18 is half, therefore if 18 is half and the brown stn'p is worth 18 then two of those stnips ought to be equal to 36. you can also use two greens, because 9 + 9 = 18 and like I said before 18 is half of the black strip, so two greens is equal to 18 plus 3 more pinks which equals 18 you would get 18 + 18 = 36. Last but not least, 2 twelves, because if 1 twelve fits half the black stnip then 2 is equal to 36.
Now we are using 3 light blue strips for the whole. It says to choose four stnips, so I will chose yellow, green, pink, and brown. So now when I compare them to the three light blue stnips it is not equal to the three light blue strips it is less. So now I will be trying yellow, green, light blue, and brown. My result is that this time it still not equal to the three light blue stnips infact it is going over by 5 squares. This time I will use brown. "9'" blue, green, pink the outcome is that I still can 't get them to equal the three light blue strips.
That's a really good explanation. Thank you for sharing where you got to with the second part. Can anyone help Ryanne?
Thank you for all these submitted solutions keep looking at other Nrich activities.
You may also like
Pies
Grandma found her pie balanced on the scale with two weights and a quarter of a pie. So how heavy was each pie?

