Linked Chains

From Westridge School in the USA we had excellent solutions sent in with pictures showing their work.

 
  


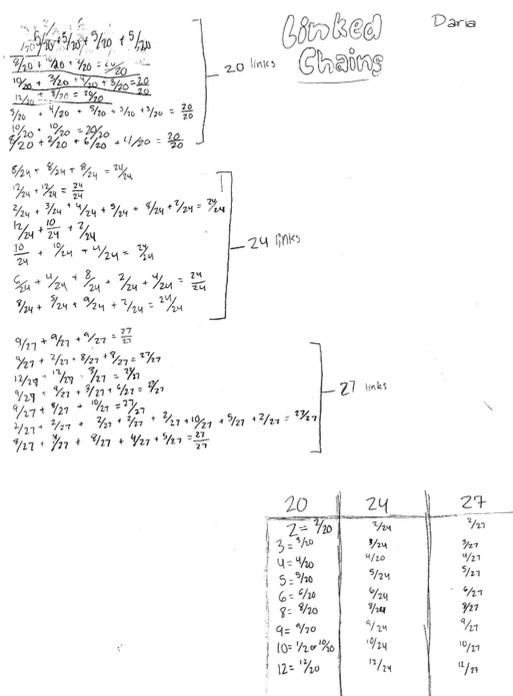
I  recommend you look at this Word file Westridge school .doc  which shows these pupils' excellent work in an easy format to read and discuss.

Also Sofie from Westridge, sent in the following,
For this problem, I first started with the example the problem showed: 1/2+1/2=1, and split each half into half, which resulted in quarters. Then I split each half, which is a chain of 5, into chains of 2 and 3. When I figured that out, I split chains of 10 (1/2) into chains of 4,6,2, and 8. Then I split those numbers other chains, like a factor tree. If you continue with this pattern, you get many results. But don't forget, there are no 1,7,or 11 chains!

Elliot and Lilly from  Husbourne Crawley Lower School wrote briefly,
We found 45 soloutions but we think there will be many more as we only had a maths lesson                                      2+8+10=20    6+6+4+4=20

Four from Thomas's Academy sent these solutions in;

Yaqub 
My way of finding out the equation is to find the equivalent fraction, so for example for finding the 24 chain link, I did 1/3+4/6  (which is the same as 8+16) because 2/6 is equal to 1/3 so 4/6 is equal to 2/3 so the equation really was 1/3+2/3 and for the other equations in the 24 chain link I did the same [I don't mean I copied the same equation I did the same method to solve the over equations] 

Hafsa
First I worked out the fractions for the 24 chain then tried a few fraction equations.1/3 + 2/3 =1.
Then I tried some more:
6/12 + 6/12 =1
6/12 =12 so 2 of those would make 24
2/3 + 2/6 =1
2/3 =16 and 2/6 =8 and 16 + 8 =24

Rihanna
First I  worked out the fractions for twenty four and used used a linked chain.
6/12+6/12=1.How I did that was 6/12 is 12 and another 6/12 is 12, so 12+12=24. 24 is one. 2/3+2/6=1 

Tyra-leighrose
First, I did 2/5+2/4+1/10= 20. Then,I did 4/8+1/2=20. Next,I did 1/2+2/4=20. After,I did 8/10+1/5=20. Finally,I did 4/5+2/10=20.[I used equivalent fractions and different strategies to solve the equations.]
To get to 24.
First, I did 6/12+3/6=24. Then,I did 4/8+1/3+1/6=24. Next, I did 2/6+1/3+4/12=24. Finally, I did 3/6+1/3=24. [I used different methods to work this out.]

Thank you all those excellent solutions which have come in for this new activity.