Skip over navigation
Using triangles
In the diagram below, horizontal and vertical dotted lines are also drawn through the centre of the rectangle. The two red triangles are congruent and so are the two yellow triangles, and the length $x$ needs to be chosen so that the area of the red triangles is equal to the area of the yellow triangles.
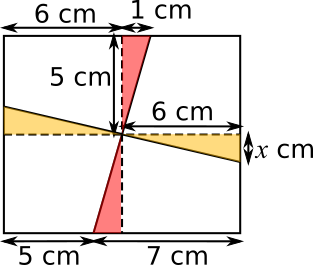
That means that $5\times1$ must be the same as $6\times x$, so $5=6x$, so $x=\dfrac{5}{6}$.
So the $10$ cm side is split into lengths of $5+\dfrac{5}{6}=5\dfrac{5}{6}$ and $5-\dfrac{5}{6}=4\dfrac{1}{6}$.
Using scale factors
Imagine if instead we had a square, as shown below. Then the sides should all be split in the same ratio to give four equal (and congruent) areas.
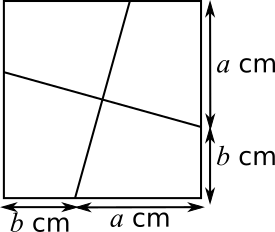
Stretching the square will give us a rectangle, and a stretch will preserve the ratio between the areas.
So starting with a $12$ cm by $12$ cm square, a vertical stretch with scale factor $\dfrac{10}{12}=\dfrac{5}{6}$ will give us the desired rectangle, and the $10$ cm side will be split into pieces of length $\dfrac{5}{6}a$ and $\dfrac{5}{6}b$ cm.
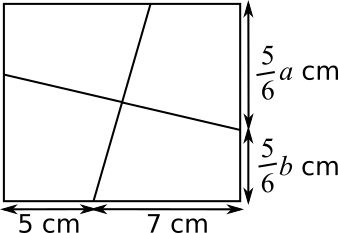
In this case, $a$ and $b$ are $7$ and $5$, so $\dfrac{5}{6}a=\dfrac{5\times7}{6}=5\dfrac{5}{6}$ and $\dfrac{5}{6}b=\dfrac{5\times5}{6}=4\dfrac{1}{6}$ cm.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Rectangle Split
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
Using triangles
In the diagram below, horizontal and vertical dotted lines are also drawn through the centre of the rectangle. The two red triangles are congruent and so are the two yellow triangles, and the length $x$ needs to be chosen so that the area of the red triangles is equal to the area of the yellow triangles.

That means that $5\times1$ must be the same as $6\times x$, so $5=6x$, so $x=\dfrac{5}{6}$.
So the $10$ cm side is split into lengths of $5+\dfrac{5}{6}=5\dfrac{5}{6}$ and $5-\dfrac{5}{6}=4\dfrac{1}{6}$.
Using scale factors
Imagine if instead we had a square, as shown below. Then the sides should all be split in the same ratio to give four equal (and congruent) areas.

Stretching the square will give us a rectangle, and a stretch will preserve the ratio between the areas.
So starting with a $12$ cm by $12$ cm square, a vertical stretch with scale factor $\dfrac{10}{12}=\dfrac{5}{6}$ will give us the desired rectangle, and the $10$ cm side will be split into pieces of length $\dfrac{5}{6}a$ and $\dfrac{5}{6}b$ cm.

In this case, $a$ and $b$ are $7$ and $5$, so $\dfrac{5}{6}a=\dfrac{5\times7}{6}=5\dfrac{5}{6}$ and $\dfrac{5}{6}b=\dfrac{5\times5}{6}=4\dfrac{1}{6}$ cm.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...

