Skip over navigation
This is the start of a spiral, starting with 1 and then moving clockwise.
For this challenge we're interested in the upper-left to lower-right diagonal, shown in green. Here is the starting example:
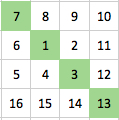
Find the numbers that would be in this green upper-left to lower-right diagonal for a spiral going up to 144 instead of just 16.
The small example above shows 7, 1, 3, 13 as the diagonal.
Now that you have a bigger diagonal going beyond 100 you need to deal with all the numbers in that diagonal in order from upper-left to lower-right.
You'll need to add the diagonal numbers in threes in order as they move through the square.
In the small example it would be 7 + 1 + 3 = 11 and 1 + 3 + 13 = 17. So your new numbers would be 11 and 17.
The totals you get for each three will give you a new set of numbers to use for Challenge 3.
You now need to use the numbers you got from adding the diagonal up in threes.
Use these numbers to make a total that has a 2 as the ones digit. You can only use a number once in any addition.
Do this in as many different ways as possible.
Do the same as in Challenge 3a but now the ones digit has to be an 8.
How many different ways are possible?
Then set challenge 2 by starting them off to ensure that as well as adding 111, 73 and 43 they'll have to add up the next three as 73, 43 and 21 (not just 21, 7, and 1), so that they have to produce ten totals altogether. (You may decide not to tell them that, but instead have some feedback from them when they have completed challenge 2).
What are you doing to try to get your totals to end in a 2 (or an 8)?
Tell me what you are doing.
What about extending the spiral past 144?
Diagonal in a Spiral
Age 7 to 11
Challenge Level 
Diagonal in a Spiral
This is the start of a spiral, starting with 1 and then moving clockwise.
For this challenge we're interested in the upper-left to lower-right diagonal, shown in green. Here is the starting example:
Challenge 1
Find the numbers that would be in this green upper-left to lower-right diagonal for a spiral going up to 144 instead of just 16.
Challenge 2
The small example above shows 7, 1, 3, 13 as the diagonal.
Now that you have a bigger diagonal going beyond 100 you need to deal with all the numbers in that diagonal in order from upper-left to lower-right.
You'll need to add the diagonal numbers in threes in order as they move through the square.
In the small example it would be 7 + 1 + 3 = 11 and 1 + 3 + 13 = 17. So your new numbers would be 11 and 17.
The totals you get for each three will give you a new set of numbers to use for Challenge 3.
Challenge 3a
You now need to use the numbers you got from adding the diagonal up in threes.
Use these numbers to make a total that has a 2 as the ones digit. You can only use a number once in any addition.
Do this in as many different ways as possible.
Challenge 3b
Do the same as in Challenge 3a but now the ones digit has to be an 8.
How many different ways are possible?
Why do this problem?
Moving through each of the challenges gives an opportunity for children to work investigatively. Children's curiosity will take them to many different places as they work on this challenge. This task is a good example that offers both a 'low threshold' starting point and at the same time offers a 'high ceiling' for those pupils who are inclined to explore much further.Possible approach
It will probably be best to have the whole group/class with you, extending together the spiral to 144.Then set challenge 2 by starting them off to ensure that as well as adding 111, 73 and 43 they'll have to add up the next three as 73, 43 and 21 (not just 21, 7, and 1), so that they have to produce ten totals altogether. (You may decide not to tell them that, but instead have some feedback from them when they have completed challenge 2).
Key questions
How are you getting your totals of three?What are you doing to try to get your totals to end in a 2 (or an 8)?
Tell me what you are doing.
Possible extension
Exploring the ten totals of threes, what can they find out?What about extending the spiral past 144?
Possible support
Some pupils may need a calculator to help with the many additions that they want to carry out.
You may also like
Prompt Cards
These two group activities use mathematical reasoning - one is numerical, one geometric.
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Exploring Wild & Wonderful Number Patterns
EWWNP means Exploring Wild and Wonderful Number Patterns Created by Yourself! Investigate what happens if we create number patterns using some simple rules.