Skip over navigation
We have created a more recent version of this task here.
We are going to look at possible jigsaw pieces.
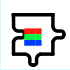
I've added the flag picture so you know which way up they go - the red at the top and the blue at the bottom. The two pairs of pieces above could look the same if you turned one around - but because the red needs to be at the top and the blue at the bottom, each piece in the pair are counted as different.
Here are three to start you off:
Before you start making/drawing/constructing pieces, think carefully and then estimate how many possible arrangements there will be and be able to explain your reasoning to others.
Jigsaw Pieces
Age 7 to 11
Challenge Level 
We have created a more recent version of this task here.
We are going to look at possible jigsaw pieces.
The kind of jigsaw we're looking at is rectangular, with straight edges.
Some of the most common jigsaw shapes are a bit like these four pieces below:
Some of the most common jigsaw shapes are a bit like these four pieces below:
I've added the flag picture so you know which way up they go - the red at the top and the blue at the bottom. The two pairs of pieces above could look the same if you turned one around - but because the red needs to be at the top and the blue at the bottom, each piece in the pair are counted as different.
So, for each jigsaw piece we start with a square template, then some sides have a peg. The edge pieces of the jigsaw have one or two straight sides.
We will only use pieces that have at least one peg and one hole.
We will only use pieces that have at least one peg and one hole.
Challenge 1
Find all the possible pieces that have at least one peg and one hole.Here are three to start you off:
Challenge 2
Again, only use pieces that have at least one peg and one hole and none the same.Find all the possible ways of making a rectangular jigsaw three pieces wide and two pieces deep, with flat edges all the way round.
Challenge 3
Read all of this one before starting!
Again, only use pieces that have at least one peg and one hole and none the same.
Find as many possible ways of making a two by four rectangular jigsaw, starting with this piece in the top left hand corner. You may also like
Little Boxes
How many different cuboids can you make when you use four CDs or DVDs? How about using five, then six?