Skip over navigation
Diamond Ring
Age 14 to 16
ShortChallenge Level 
The diagram below shows the diagonals:
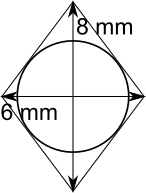
The diagonals of a rhombus cross at right angles, so four right-angled triangles are formed, as shown below (all lengths are in mm).
The hypotenuse of the right-angled triangle can be found using Pythagoras' Theorem. $$\begin{align}4^2+3^2&=c^2\\
\Rightarrow25&=c^2\\
\Rightarrow5&=c\end{align}$$
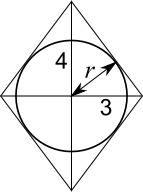
Just looking at that triangle, note that the radius meets the tangent at a right angle, so two smaller right-angled triangles are formed, as shown below.
Each of the smaller right-angled triangles shares an angle with the larger right-angled triangle, so the three triangles are all similar. $r$ can be found using either triangle.
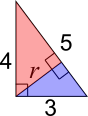
Consider the red triangle:
Its hypotenuse is $4$mm and the hypotenuse of the largest triangle is $5$mm, so the scale factor is $\frac{4}{5}$
$r$ is the shortest side of the red triangle, so $r=\frac{4}{5}\times 3 =2.4$ mm.
Consider the blue triangle:
Its hypotenuse is $3$mm and the hypotenuse of the largest triangle is $5$mm, so the scale factor is $\frac{3}{5}$
$r$ is the longer side of the blue triangle, so $r=\frac{3}{5}\times 4 = 2.4$ mm.
Alternatively, note that the area of the right-angled triangle is $3 \times 4=12\text{mm}^2$. We could also work out the area of the triangle by considering it to have a base of $5$ and a height of $r$, so $5r=12$ so $r=\frac{12}5=2.4$mm
The diagonals of a rhombus cross at right angles, so four right-angled triangles are formed, as shown below (all lengths are in mm).
The hypotenuse of the right-angled triangle can be found using Pythagoras' Theorem. $$\begin{align}4^2+3^2&=c^2\\
\Rightarrow25&=c^2\\
\Rightarrow5&=c\end{align}$$
Just looking at that triangle, note that the radius meets the tangent at a right angle, so two smaller right-angled triangles are formed, as shown below.
Each of the smaller right-angled triangles shares an angle with the larger right-angled triangle, so the three triangles are all similar. $r$ can be found using either triangle.
Consider the red triangle:
Its hypotenuse is $4$mm and the hypotenuse of the largest triangle is $5$mm, so the scale factor is $\frac{4}{5}$
$r$ is the shortest side of the red triangle, so $r=\frac{4}{5}\times 3 =2.4$ mm.
Consider the blue triangle:
Its hypotenuse is $3$mm and the hypotenuse of the largest triangle is $5$mm, so the scale factor is $\frac{3}{5}$
$r$ is the longer side of the blue triangle, so $r=\frac{3}{5}\times 4 = 2.4$ mm.
Alternatively, note that the area of the right-angled triangle is $3 \times 4=12\text{mm}^2$. We could also work out the area of the triangle by considering it to have a base of $5$ and a height of $r$, so $5r=12$ so $r=\frac{12}5=2.4$mm
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
Bendy Quad
Four rods are hinged at their ends to form a convex quadrilateral. Investigate the different shapes that the quadrilateral can take. Be patient this problem may be slow to load.
