Skip over navigation
Answer: a loss (of £21,000)
House which made a loss: lost 20% of an original price higher than £252,000
House which made a profit: gained 20% of an original price lower than £252,000
Lost 20% of a higher number and gained 20% of a lower number $\Rightarrow$ loss overall.
This is shown in the diagram below.
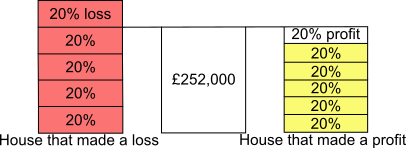
Using the diagram to find the value of the loss
Looking at the left hand side of the diagram, £252,000 is equal to 4$\times$the 20% loss.
So the loss was £252,000$\div$4 = £63,000.
Looking at the right hand side of the diagram, £252,000 is equal to 6$\times$the 20% profit.
So the profit was £252,000$\div$6 = £42,000.
So the overall loss was £63,000$-$ £42,00 = £21,000.
Using fractions to find the value of the loss
20% is the same as $\frac{1}{5}$, so the house that made a loss was sold at $\frac{4}{5}$ of its original price and the house that made a profit was sold at $\frac{6}{5}$ of its original price.
So if the house that made a loss was bought for £$L$, then $$\begin{align}252\hspace{1mm}000&=\frac{4}{5}L\\
\Rightarrow 252\hspace{1mm}\times5\div4&=L\\
\Rightarrow315\hspace{1mm}000&=L\end{align}$$
And if the house that made a profit was bought for £$P$, then $$\begin{align}252\hspace{1mm}000&=\frac{6}{5}P\\
\Rightarrow 252\hspace{1mm}\times5\div6&=P\\
\Rightarrow210\hspace{1mm}000&=P\end{align}$$
So the developer spent £315,000 + £210,000 = £525,000, and took £252,000$\times$2 = £504,000, which gives a total loss of £21,000.
Using multiplication and division to find the value of the loss
A $20\%$ price decrease corresponds to multiplying by $0.8$, so if the house that made a loss was bought for £$L$, then $L\times0.8=252\hspace{1mm}000,$ so $L=252\hspace{1mm}000\div0.8.$
”‹A $20\%$ price increase corresponds to multiplying by $1.2$, so if the house that made a profit was bought for £$P$, then $P\times1.2=252\hspace{1mm}000,$ so $P=252\hspace{1mm}000\div1.2.$
So the total profit was $\dfrac{252\hspace{1mm}000}{0.8}+\dfrac{252\hspace{1mm}000}{1.2}-252\hspace{1mm}000\times2=-21\hspace{1mm}000$ - which is a loss of £$21,000.$
Note: writing $252,000$ as $A$ in the expression above gives a profit of $\dfrac{A}{0.8}+\dfrac{A}{1.2}-2A=A\times\left(\dfrac{1}{0.8}+\dfrac{1}{1.2}-2\right)=A\times-0.08\dot{3}$. So the loss is always $8.\dot{3}$% of the selling price of the houses.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
The Property Market
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Answer: a loss (of £21,000)
House which made a loss: lost 20% of an original price higher than £252,000
House which made a profit: gained 20% of an original price lower than £252,000
Lost 20% of a higher number and gained 20% of a lower number $\Rightarrow$ loss overall.
This is shown in the diagram below.

Using the diagram to find the value of the loss
Looking at the left hand side of the diagram, £252,000 is equal to 4$\times$the 20% loss.
So the loss was £252,000$\div$4 = £63,000.
Looking at the right hand side of the diagram, £252,000 is equal to 6$\times$the 20% profit.
So the profit was £252,000$\div$6 = £42,000.
So the overall loss was £63,000$-$ £42,00 = £21,000.
Using fractions to find the value of the loss
20% is the same as $\frac{1}{5}$, so the house that made a loss was sold at $\frac{4}{5}$ of its original price and the house that made a profit was sold at $\frac{6}{5}$ of its original price.
So if the house that made a loss was bought for £$L$, then $$\begin{align}252\hspace{1mm}000&=\frac{4}{5}L\\
\Rightarrow 252\hspace{1mm}\times5\div4&=L\\
\Rightarrow315\hspace{1mm}000&=L\end{align}$$
And if the house that made a profit was bought for £$P$, then $$\begin{align}252\hspace{1mm}000&=\frac{6}{5}P\\
\Rightarrow 252\hspace{1mm}\times5\div6&=P\\
\Rightarrow210\hspace{1mm}000&=P\end{align}$$
So the developer spent £315,000 + £210,000 = £525,000, and took £252,000$\times$2 = £504,000, which gives a total loss of £21,000.
Using multiplication and division to find the value of the loss
A $20\%$ price decrease corresponds to multiplying by $0.8$, so if the house that made a loss was bought for £$L$, then $L\times0.8=252\hspace{1mm}000,$ so $L=252\hspace{1mm}000\div0.8.$
”‹A $20\%$ price increase corresponds to multiplying by $1.2$, so if the house that made a profit was bought for £$P$, then $P\times1.2=252\hspace{1mm}000,$ so $P=252\hspace{1mm}000\div1.2.$
So the total profit was $\dfrac{252\hspace{1mm}000}{0.8}+\dfrac{252\hspace{1mm}000}{1.2}-252\hspace{1mm}000\times2=-21\hspace{1mm}000$ - which is a loss of £$21,000.$
Note: writing $252,000$ as $A$ in the expression above gives a profit of $\dfrac{A}{0.8}+\dfrac{A}{1.2}-2A=A\times\left(\dfrac{1}{0.8}+\dfrac{1}{1.2}-2\right)=A\times-0.08\dot{3}$. So the loss is always $8.\dot{3}$% of the selling price of the houses.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
Bendy Quad
Four rods are hinged at their ends to form a convex quadrilateral. Investigate the different shapes that the quadrilateral can take. Be patient this problem may be slow to load.

