Skip over navigation
This activity follows on from More Fraction Bars.
Look at these different coloured bars:
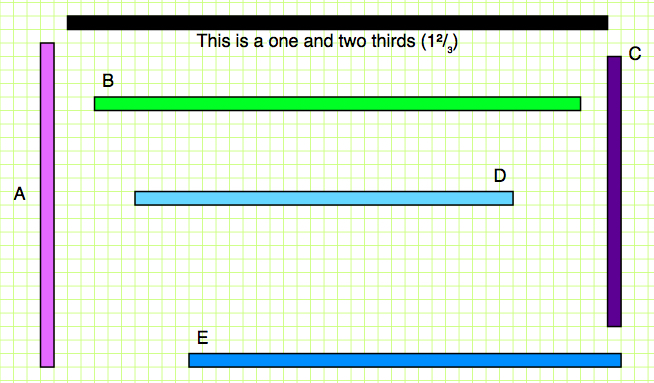
You might like to download a printable version of them here .
Put the bars in size order - can you do it without cutting them out?
Now focus on this bar:

This bar represents one whole and two thirds, or the number 1$\frac{2}{3}$. You might find it easier to think of it as a bar which is 'one whole' that has been stuck to a bar two-thirds the size of it.
We are thinking about all the other coloured bars as fractions of this bar, so we are thinking about them as fractions of 1$\frac{2}{3}$.
For example, look at Bar A below:

Drawing lines helps us measure it against the black bar:

What fraction of the black bar is Bar A?
Go through each of the other coloured bars and compare them to the black bar. What fraction of 1$\frac{2}{3}$ is each bar?
Write down your ideas for each bar. For example, you could write:
Bar A is three fifths of the black bar.
or
Bar A represents $\frac{3}{5}$ of 1$\frac{2}{3}$.
or
Bar A represents a whole.
Can you work out how we came up with these three ideas?
Can you find different ideas for what fraction of 1$\frac{2}{3}$ each bar represents?

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Extending Fraction Bars
Age 7 to 11
Challenge Level 





This activity follows on from More Fraction Bars.
Look at these different coloured bars:

You might like to download a printable version of them here .
Put the bars in size order - can you do it without cutting them out?
Now focus on this bar:

This bar represents one whole and two thirds, or the number 1$\frac{2}{3}$. You might find it easier to think of it as a bar which is 'one whole' that has been stuck to a bar two-thirds the size of it.
We are thinking about all the other coloured bars as fractions of this bar, so we are thinking about them as fractions of 1$\frac{2}{3}$.
For example, look at Bar A below:

Drawing lines helps us measure it against the black bar:

What fraction of the black bar is Bar A?
Go through each of the other coloured bars and compare them to the black bar. What fraction of 1$\frac{2}{3}$ is each bar?
Write down your ideas for each bar. For example, you could write:
Bar A is three fifths of the black bar.
or
Bar A represents $\frac{3}{5}$ of 1$\frac{2}{3}$.
or
Bar A represents a whole.
Can you work out how we came up with these three ideas?
Can you find different ideas for what fraction of 1$\frac{2}{3}$ each bar represents?
You may also like
Pies
Grandma found her pie balanced on the scale with two weights and a quarter of a pie. So how heavy was each pie?

