Skip over navigation
This activity follows on from Complex Puzzle.
Use the Geogebra interactivity below to find some pairs of complex numbers whose product is a real number. What do you notice?
Can you explain it algebraically?
Use the Geogebra interactivity to find some pairs of complex numbers whose product is an imaginary number. What do you notice?
Can you explain it algebraically?
In general, what would you need to multiply by $a+bi$ to get a real number? Or to get an imaginary number?
For a given complex number $a + bi$, what would you need to multiply by to get to another given number $x + yi$?
How does this relate to your geometric interpretation of multiplication of complex numbers?
Mapping the Territory
Age 14 to 18
Challenge Level 
This resource is part of our Adventures with Complex Numbers collection
This activity follows on from Complex Puzzle.
Use the Geogebra interactivity below to find some pairs of complex numbers whose product is a real number. What do you notice?
Can you explain it algebraically?
Use the Geogebra interactivity to find some pairs of complex numbers whose product is an imaginary number. What do you notice?
Can you explain it algebraically?
In general, what would you need to multiply by $a+bi$ to get a real number? Or to get an imaginary number?
For a given complex number $a + bi$, what would you need to multiply by to get to another given number $x + yi$?
How does this relate to your geometric interpretation of multiplication of complex numbers?
You may also like
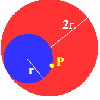
Just Rolling Round
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
30-60-90 Polypuzzle
Re-arrange the pieces of the puzzle to form a rectangle and then to form an equilateral triangle. Calculate the angles and lengths.