Skip over navigation
Answer: 7
Using trial and improvement
Ones (units) column: E + E gives S
Tens column: E + E gives E
So E + E must be 10 or more, so that 1 is carried to give a different result in the two columns
Try E = 5
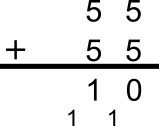 E can't be 5, because should have E in the tens column
E can't be 5, because should have E in the tens column
Try E = 6
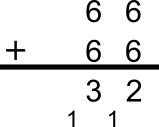 E should be larger
E should be larger
Try E = 8
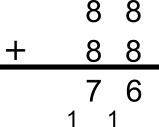 E should be larger
E should be larger
Try E = 9
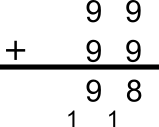
That works, so E must be 9, and S must be 8. So we have
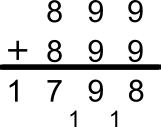
And X = 7.
Using algebra
Notice that the ones (units) column has $E + E$ and gives $S$, but in the tens column, $E + E$ gives $E$. So $E + E$ must be $10$ or more, so that $1$ is carried to give a different result in the tens column.
So $E + E = 10 + S$, and $E + E + 1 = 10 + E$.
$E + E + 1 = 10 + E$ means that $E + 1 = 10$, so $E = 9$.
So since $E + E = 10 + S$, $18 = 10 + S$, so $S = 8$.
So we have

And so $X=7$.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
See Axes
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
Answer: 7
Using trial and improvement
Ones (units) column: E + E gives S
Tens column: E + E gives E
So E + E must be 10 or more, so that 1 is carried to give a different result in the two columns
Try E = 5
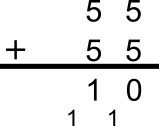 E can't be 5, because should have E in the tens column
E can't be 5, because should have E in the tens columnTry E = 6
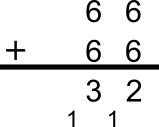 E should be larger
E should be largerTry E = 8
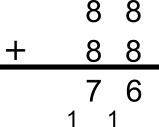 E should be larger
E should be largerTry E = 9
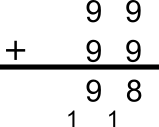
That works, so E must be 9, and S must be 8. So we have

And X = 7.
Using algebra
Notice that the ones (units) column has $E + E$ and gives $S$, but in the tens column, $E + E$ gives $E$. So $E + E$ must be $10$ or more, so that $1$ is carried to give a different result in the tens column.
So $E + E = 10 + S$, and $E + E + 1 = 10 + E$.
$E + E + 1 = 10 + E$ means that $E + 1 = 10$, so $E = 9$.
So since $E + E = 10 + S$, $18 = 10 + S$, so $S = 8$.
So we have

And so $X=7$.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...

