Skip over navigation

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Diagonal Side
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
Measuring using unit squares
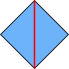 The side length of the square is equal to the diagonal of the unit square, as shown in the diagram on the right, where the red length is the side of the new square and the blue square is a unit square.
The side length of the square is equal to the diagonal of the unit square, as shown in the diagram on the right, where the red length is the side of the new square and the blue square is a unit square.
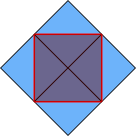
 Sticking four of these together, as shown on the left, draws the whole square. The unit squares fit perfectly together as the red lines split them in half, and so each angle is 90$^\text o $
or 45$^\text o$.
Sticking four of these together, as shown on the left, draws the whole square. The unit squares fit perfectly together as the red lines split them in half, and so each angle is 90$^\text o $
or 45$^\text o$.
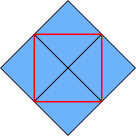
The area of the square is shaded in the diagram on the right. It contains four half-unit-squares - so its area is four half-units, or two whole units.
Using Pythagoras' Theorem to find the side length
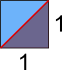 If this square is a unit square, then its diagonal, shown in red, will be the side length of the square.
If this square is a unit square, then its diagonal, shown in red, will be the side length of the square.
Applying Pythagoras' Theorem to the triangle will give us information about this length, here called $c$: $1^2+1^2=c^2\Rightarrow2=c^2$
But $c^2$ is the area of the square with side length $c$. So if $c^2=2$, then the area is $2$.
 The side length of the square is equal to the diagonal of the unit square, as shown in the diagram on the right, where the red length is the side of the new square and the blue square is a unit square.
The side length of the square is equal to the diagonal of the unit square, as shown in the diagram on the right, where the red length is the side of the new square and the blue square is a unit square.
 Sticking four of these together, as shown on the left, draws the whole square. The unit squares fit perfectly together as the red lines split them in half, and so each angle is 90$^\text o $
or 45$^\text o$.
Sticking four of these together, as shown on the left, draws the whole square. The unit squares fit perfectly together as the red lines split them in half, and so each angle is 90$^\text o $
or 45$^\text o$.The area of the square is shaded in the diagram on the right. It contains four half-unit-squares - so its area is four half-units, or two whole units.
Using Pythagoras' Theorem to find the side length
 If this square is a unit square, then its diagonal, shown in red, will be the side length of the square.
If this square is a unit square, then its diagonal, shown in red, will be the side length of the square. Applying Pythagoras' Theorem to the triangle will give us information about this length, here called $c$: $1^2+1^2=c^2\Rightarrow2=c^2$
But $c^2$ is the area of the square with side length $c$. So if $c^2=2$, then the area is $2$.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Hallway Borders
What are the possible dimensions of a rectangular hallway if the number of tiles around the perimeter is exactly half the total number of tiles?

