Space Distances
Space Distances
In the picture below you can see the orbits of Mercury, Venus, Earth (this label is slightly hidden) and Mars, along with the orbit of an asteroid called Florence (named after Florence Nightingale).
The picture shows their positions in August 2017. Florence was at its nearest position to Earth at the start of September 2017.
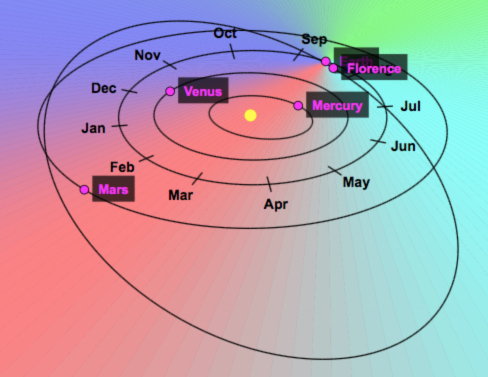
Florence's distance from the Sun varies from 150 000 000km at its nearest (during summer 2017) to 375 000 000km when furthest away.
Starting when Florence is nearest to the sun, what distance will it be from the Sun after travelling...
1) 100 km further from the Sun?
2) 1 000 km further from the Sun?
3) 10 000 km further from the Sun?
4) 100 000 km further from the Sun?
5) 1 000 000 km further from the Sun?
Starting with Florence furthest from the sun, what distance will it be from the Sun after travelling...
6) 100 km nearer the Sun?
7) 1 000 km nearer the Sun?
8) 10 000 km nearer the Sun?
9) 100 000 km nearer the Sun?
10) 1 000 000 km nearer the Sun?
Why do this problem?
This activity offers an opportunity to count forwards and/or backwards in steps of powers of ten.
Possible approach
Present the picture and ask the group to 'say what they see'. This allows all children to take part and sets the scene for the task. You will need to provide them with some of the information given in the text and then you can faciliate a discussion about Florence's journey.
You may wish to tackle the questions as a whole group, perhaps giving children time to think individually before talking to a partner, then sharing with everyone.
Key questions
How are you working out your answers?
Could you think of some other questions to ask about this?
Possible extension
Ask the pupils to think up their own challenges to give one another but they need to know the correct answers themselves!
You may also like
Pebbles
Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?
Bracelets
Investigate the different shaped bracelets you could make from 18 different spherical beads. How do they compare if you use 24 beads?
Sweets in a Box
How many different shaped boxes can you design for 36 sweets in one layer? Can you arrange the sweets so that no sweets of the same colour are next to each other in any direction?