Skip over navigation
First, it is necessary to work out where B is.
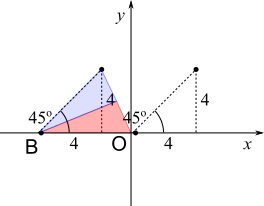
Since A is 4 up and 4 along from the origin, OA makes a $45^\circ$ angle with the $x$ axis. This means that the obtuse angle between OA and the $x$ axis must be $135^\circ$, so B must lie on the $x$ axis. This is shown in the diagrams below, where the red triangle is the triangle whose area we need to find.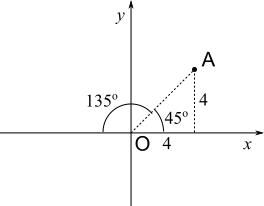
The distances OA and OB are equal, since OB is just a rotation of OA. This distance can be found by considering the triangle below:
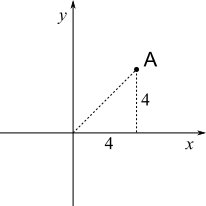
This triangle is right-angled and OA is the hypotenuse, so, by Pythagoras' Theorem,
${\text{OA}}^2=4^2+4^2=2\times4^2$ or $32$,
So $\text{OA}=\sqrt{32}=5.657$ or $4\sqrt2$.
Now, there are various different possible methods.
Using the area of a triangle formula
Area = $\frac12$ base x height
= $\frac12$ OB x $y$ coordinate of A
= $\frac12$ x $4\sqrt2$ x 4
= $8\sqrt2$
Using horizontal and vertical triangles and rectangles
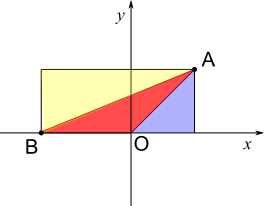
The yellow and blue triangles are drawn to make a rectangle with the red triangle. The length of the rectangle is OB plus the $x$ coordinate of A, so it is $4+4\sqrt2$ or $4+5.66=9.657$
The height of the rectangle is the $y$ coordinate of A, which is $4$.
So the area of the rectangle is $4(4+4\sqrt2)=16+16\sqrt2$ square units, or $4\times9.657=38.63$ square units.
The area of the yellow triangle is half of the area of the rectangle, so the area of the red and blue triangles combined is also equal to half the area of the rectangle. That area is $(16+16\sqrt2)\div2=8+8\sqrt2$, or $38.63\div2=19.31$, square units.
The blue triangle has base $4$ and heght $4$, so its area is $\frac124\times4=8$ square units.
So the area of the red triangle is $8+8\sqrt2-8=8\sqrt2$, or $19.31-8=11.31$, square units.
Using trigonometry
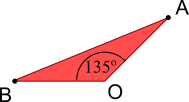This triangle is perfect for the formula $\text{Area}=\frac12ab\sin{C}$, where:
$a=b=4\sqrt2$ or $5.657$, and $C=135^\circ$
So $\text{Area}=\frac12(4\sqrt2)^2\sin{135}=8\sqrt2$ square units.
Cutting up the triangle and rearranging the pieces
The triangle is isosceles, so the angles at A and B are equal. Since all of the angles add up to $180^\circ$, these angles must add up to $45^\circ$, or must be $22.5^\circ$ each.
Now imagine cutting the triangle in half along the dotted line, and then rotating the blue part, so that the two
$22.5^\circ$ angles join up to make a $45^\circ$ angle, as shown.
Notice that the triangle is still isosceles, because the image of OA is the side sloping upwards from B.
Comparing this to the original position of A, notice that really it's just a translation, because of the $45^\circ$ angle formed. So the height of the new triangle is $4$ units.
The base of the new triangle is still OB, which is $4\sqrt2$ os $5.657$ units.
So the area of the new triangle is $\frac12\times4\times4\sqrt2=8\sqrt2$ or $\frac12\times4\times5.657=11.31$ square units.
What happens if you apply the formula $\text{Area}=\frac12ab\sin{C}$ to this new triangle? How does this compare to the answer you get if you use the trigonometry method above?
Rotation and Area
Age 14 to 16
ShortChallenge Level 
First, it is necessary to work out where B is.
Since A is 4 up and 4 along from the origin, OA makes a $45^\circ$ angle with the $x$ axis. This means that the obtuse angle between OA and the $x$ axis must be $135^\circ$, so B must lie on the $x$ axis. This is shown in the diagrams below, where the red triangle is the triangle whose area we need to find.
The distances OA and OB are equal, since OB is just a rotation of OA. This distance can be found by considering the triangle below:
This triangle is right-angled and OA is the hypotenuse, so, by Pythagoras' Theorem,
${\text{OA}}^2=4^2+4^2=2\times4^2$ or $32$,
So $\text{OA}=\sqrt{32}=5.657$ or $4\sqrt2$.
Now, there are various different possible methods.
Using the area of a triangle formula
Area = $\frac12$ base x height
= $\frac12$ OB x $y$ coordinate of A
= $\frac12$ x $4\sqrt2$ x 4
= $8\sqrt2$
Using horizontal and vertical triangles and rectangles
The yellow and blue triangles are drawn to make a rectangle with the red triangle. The length of the rectangle is OB plus the $x$ coordinate of A, so it is $4+4\sqrt2$ or $4+5.66=9.657$
The height of the rectangle is the $y$ coordinate of A, which is $4$.
So the area of the rectangle is $4(4+4\sqrt2)=16+16\sqrt2$ square units, or $4\times9.657=38.63$ square units.
The area of the yellow triangle is half of the area of the rectangle, so the area of the red and blue triangles combined is also equal to half the area of the rectangle. That area is $(16+16\sqrt2)\div2=8+8\sqrt2$, or $38.63\div2=19.31$, square units.
The blue triangle has base $4$ and heght $4$, so its area is $\frac124\times4=8$ square units.
So the area of the red triangle is $8+8\sqrt2-8=8\sqrt2$, or $19.31-8=11.31$, square units.
Using trigonometry
This triangle is perfect for the formula $\text{Area}=\frac12ab\sin{C}$, where:$a=b=4\sqrt2$ or $5.657$, and $C=135^\circ$
So $\text{Area}=\frac12(4\sqrt2)^2\sin{135}=8\sqrt2$ square units.
Cutting up the triangle and rearranging the pieces
The triangle is isosceles, so the angles at A and B are equal. Since all of the angles add up to $180^\circ$, these angles must add up to $45^\circ$, or must be $22.5^\circ$ each.
Now imagine cutting the triangle in half along the dotted line, and then rotating the blue part, so that the two
$22.5^\circ$ angles join up to make a $45^\circ$ angle, as shown.Notice that the triangle is still isosceles, because the image of OA is the side sloping upwards from B.
Comparing this to the original position of A, notice that really it's just a translation, because of the $45^\circ$ angle formed. So the height of the new triangle is $4$ units.The base of the new triangle is still OB, which is $4\sqrt2$ os $5.657$ units.
So the area of the new triangle is $\frac12\times4\times4\sqrt2=8\sqrt2$ or $\frac12\times4\times5.657=11.31$ square units.
What happens if you apply the formula $\text{Area}=\frac12ab\sin{C}$ to this new triangle? How does this compare to the answer you get if you use the trigonometry method above?
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Some(?) of the Parts
A circle touches the lines OA, OB and AB where OA and OB are perpendicular. Show that the diameter of the circle is equal to the perimeter of the triangle
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
Bendy Quad
Four rods are hinged at their ends to form a convex quadrilateral. Investigate the different shapes that the quadrilateral can take. Be patient this problem may be slow to load.