Skip over navigation
Sketch diagram
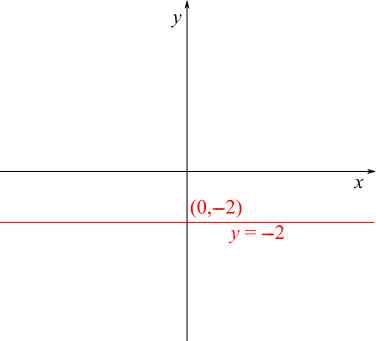
$y=-2$ means that the $y$ coordinate will always be $-2$, regardless of what $x$ is. So this is the line through $(3,-2)$, $(-6,-2)$, $(0,-2)$ and $(1000000,-2)$ - that is, a horizontal line 'along' $-2$:
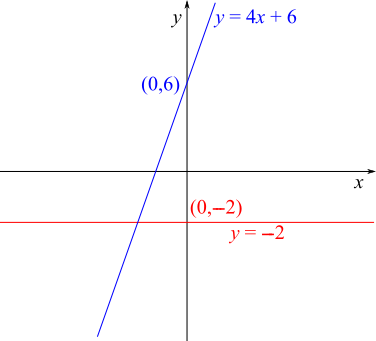
Next, $y=4x+6$ has gradient $4$ and $y$-intercept $6$ - so it slopes up steeply and crosses the $y$ axis at $(0,6)$.
Next, $x+y=6$ has gradient $-1$ and $y$ intercept $6$ ($x+y=6$ is the same as $y=-x+6$). So it slopes downwards, much more gently than the blue line, and also crosses the $y$ axis at $(0,6)$:
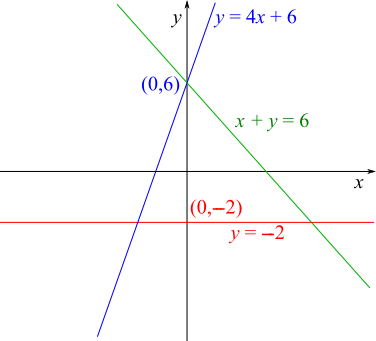
You can already see that the height of the triangle is $8$ units, from $-2$ to $6$ on the $y$ axis.
For the base of the triangle...
Finding the coordinates of the points of intersection
Suppose $y=-2$ and $y=4x+6$ intersect at some point $(a,b)$.
$(a,b)$ is on the line $y=-2$, so $b=-2$.
$(a,b)$ is on the line $y=4x+6$, so $b=4a+6$. But $b=-2$, so $-2=4a+6\Rightarrow -8=4a\Rightarrow -2=a$.
So $y=-2$ and $y=4x+6$ intersect at $(-2,-2)$.
Suppose $y=-2$ and $x+y=6$ intersect at some point $(c,d)$.
$(c,d)$ is on the line $y=-2$, so $d=-2$.
$(c,d)$ is on the line $x+y=6$, so $c+d=6$. But $d=-2$, so $c-2=6\Rightarrow c=8$.
So $y=-2$ and $x+y=6$ intersect at $(8,-2)$. This is shown below.
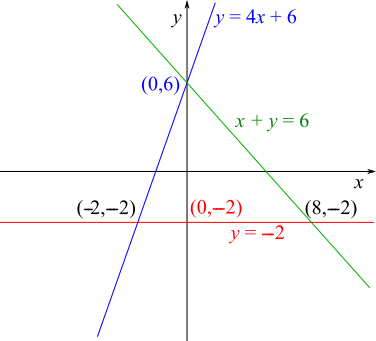
So the base of the triangle is from $x=-2$ to $x=8$, which is $10$ units.
So the area of the triangle is $\frac12\times8\times10=40$ square units.
Using gradients
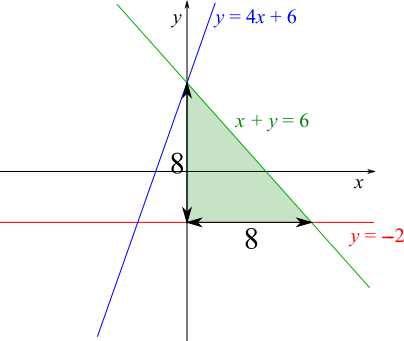 The gradient of the line $x+y=6$ is $-1$, so when going down $8$ units from the top to the bottom of the triangle, it must also go along $8$ units, as shown on the right.
The gradient of the line $x+y=6$ is $-1$, so when going down $8$ units from the top to the bottom of the triangle, it must also go along $8$ units, as shown on the right.
The line $y=4x+6$ has gradient $4$, so it is $4$ times steeper. This means that going down by the same amount corresponds to going $4$ times less far along.
So the base of the blue triangle shown below is only $8\div4=2$ units.
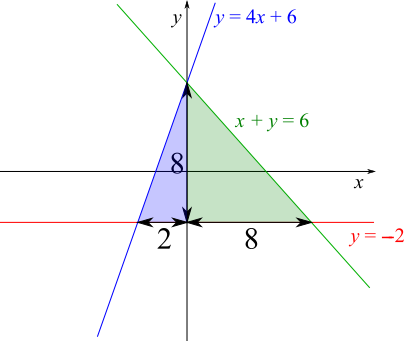 We could find the areas of the green and blue triangles separately, or of the whole triangle, whose base is $10$ units in total.
We could find the areas of the green and blue triangles separately, or of the whole triangle, whose base is $10$ units in total.
Green triangle: $\frac12\times8\times8=32$ square units
Blue triangle: $\frac12\times8\times2=8$ square units
Whole triangle: $32+8=40$ square units, or $\frac12\times8\times10=40$ square units.
Plotting the lines on a grid
Plotting the lines carefully, you can find the dimensions of the triangle.
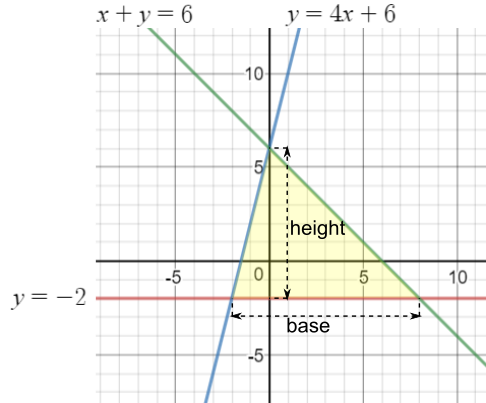
Now, you can count that the base is $10$ units and the height is $8$ units, so the area is $\frac12\times8\times10=40$ square units.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Linear Area
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
Sketch diagram
$y=-2$ means that the $y$ coordinate will always be $-2$, regardless of what $x$ is. So this is the line through $(3,-2)$, $(-6,-2)$, $(0,-2)$ and $(1000000,-2)$ - that is, a horizontal line 'along' $-2$:

Next, $y=4x+6$ has gradient $4$ and $y$-intercept $6$ - so it slopes up steeply and crosses the $y$ axis at $(0,6)$.

Next, $x+y=6$ has gradient $-1$ and $y$ intercept $6$ ($x+y=6$ is the same as $y=-x+6$). So it slopes downwards, much more gently than the blue line, and also crosses the $y$ axis at $(0,6)$:

You can already see that the height of the triangle is $8$ units, from $-2$ to $6$ on the $y$ axis.
For the base of the triangle...
Finding the coordinates of the points of intersection
Suppose $y=-2$ and $y=4x+6$ intersect at some point $(a,b)$.
$(a,b)$ is on the line $y=-2$, so $b=-2$.
$(a,b)$ is on the line $y=4x+6$, so $b=4a+6$. But $b=-2$, so $-2=4a+6\Rightarrow -8=4a\Rightarrow -2=a$.
So $y=-2$ and $y=4x+6$ intersect at $(-2,-2)$.
Suppose $y=-2$ and $x+y=6$ intersect at some point $(c,d)$.
$(c,d)$ is on the line $y=-2$, so $d=-2$.
$(c,d)$ is on the line $x+y=6$, so $c+d=6$. But $d=-2$, so $c-2=6\Rightarrow c=8$.
So $y=-2$ and $x+y=6$ intersect at $(8,-2)$. This is shown below.

So the base of the triangle is from $x=-2$ to $x=8$, which is $10$ units.
So the area of the triangle is $\frac12\times8\times10=40$ square units.
Using gradients
 The gradient of the line $x+y=6$ is $-1$, so when going down $8$ units from the top to the bottom of the triangle, it must also go along $8$ units, as shown on the right.
The gradient of the line $x+y=6$ is $-1$, so when going down $8$ units from the top to the bottom of the triangle, it must also go along $8$ units, as shown on the right.The line $y=4x+6$ has gradient $4$, so it is $4$ times steeper. This means that going down by the same amount corresponds to going $4$ times less far along.
So the base of the blue triangle shown below is only $8\div4=2$ units.
 We could find the areas of the green and blue triangles separately, or of the whole triangle, whose base is $10$ units in total.
We could find the areas of the green and blue triangles separately, or of the whole triangle, whose base is $10$ units in total.Green triangle: $\frac12\times8\times8=32$ square units
Blue triangle: $\frac12\times8\times2=8$ square units
Whole triangle: $32+8=40$ square units, or $\frac12\times8\times10=40$ square units.
Plotting the lines on a grid
Plotting the lines carefully, you can find the dimensions of the triangle.

Now, you can count that the base is $10$ units and the height is $8$ units, so the area is $\frac12\times8\times10=40$ square units.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
Related Collections
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...

