Skip over navigation
Can you work out the angles in the pictures below?
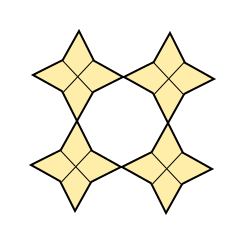
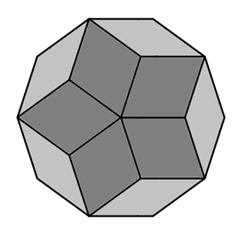
On the left, a regular octagon is surrounded by congruent kites. On the right, a regular decagon is divided into two different types of rhombuses.
Here are two more polygon puzzles to try.
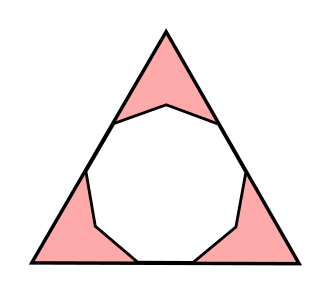
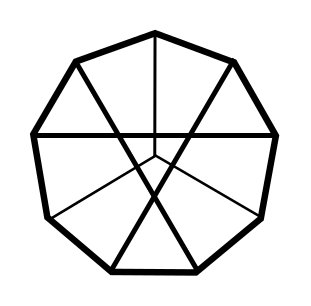
The first one is a regular nonagon drawn inside an equilateral triangle. The second is also a regular nonagon, with lines joining vertices to each other and to the centre.
Can you work out the angles?
The game of Shogi, also known as Japanese Chess, is played with tiles on a 9 by 9 board.
Here is a picture of some Shogi pieces that have been arranged in a pattern:

What questions might a mathematician ask?
Here are some that we thought of:
Can you come up with answers to any of your questions?
Can you justify your answers?
Thanks to Percy Henderson who shared with us his exploration of Shogi tiles and kindly granted permission to use his picture, and to Don Steward for the ideas behind the other polygon puzzles.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Shogi Shapes
Age 11 to 14
Challenge Level 





Can you work out the angles in the pictures below?
On the left, a regular octagon is surrounded by congruent kites. On the right, a regular decagon is divided into two different types of rhombuses.


Here are two more polygon puzzles to try.
The first one is a regular nonagon drawn inside an equilateral triangle. The second is also a regular nonagon, with lines joining vertices to each other and to the centre.
Can you work out the angles?


The game of Shogi, also known as Japanese Chess, is played with tiles on a 9 by 9 board.
Here is a picture of some Shogi pieces that have been arranged in a pattern:

What questions might a mathematician ask?
Here are some that we thought of:
- Is there a quick way to count the number of tiles in the picture?
- What shape are the tiles?
- Which angles can be calculated?
- If we assume that the tiles are symmetrical, there are two pairs of matching angles and one other angle. What is the range of possible sizes of that "lonely" angle?
- Could we make other sets where we need more tiles to go all the way round with no gaps?
Can you come up with answers to any of your questions?
Can you justify your answers?
Thanks to Percy Henderson who shared with us his exploration of Shogi tiles and kindly granted permission to use his picture, and to Don Steward for the ideas behind the other polygon puzzles.
You may also like
On Time
On a clock the three hands - the second, minute and hour hands - are on the same axis. How often in a 24 hour day will the second hand be parallel to either of the two other hands?
LOGO Challenge 1 - Star Square
Can you use LOGO to create this star pattern made from squares. Only basic LOGO knowledge needed.

