Skip over navigation
Answer: 3025
The sequence of all floors






Even floors: 2 purple tiles per row (total number even)
Odd floors: 1 more purple tile than the previous floor (total number odd)
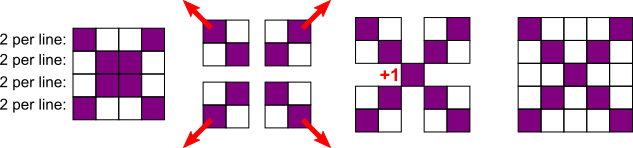
109 purple tiles
108 = 2$\times$54 so floor length 54 has 108 purple tiles
$\therefore$ floor length 55 has 108 + 1 = 109 purple tiles
Floor length 55 has 55$^2$ = 3025 tiles
The sequence of odd-sided floors
Each odd-sided floor contains the last odd-sided floor in the middle, outlined in blue.



4 purple tiles are added each time
Side length 2 longer each time
109 = 1 + 4$\times$?
= 1 + 108
= 1 + 4$\times$27
So side length = 1 + 2$\times$27 = 55
$\therefore$ total number of tiles = 55$^2$ = 3025
Finding the number of rows
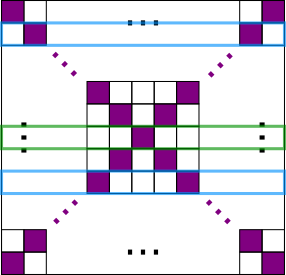 There are 2 purple tiles on each row,
There are 2 purple tiles on each row,
Except for the middle row which has 1 purple tile (on odd-sided floors)
109 tiles = 1 purple tile in the middle
+ 108 purple tiles in pairs
= 1 purple tile in the middle
+ 54 pairs on 54 rows
$\therefore$ there are 1 + 54 = 55 rows
So there are 55$^2$ = 3025 tiles



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Tiled Floor
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
Answer: 3025
The sequence of all floors






Even floors: 2 purple tiles per row (total number even)
Odd floors: 1 more purple tile than the previous floor (total number odd)

109 purple tiles
108 = 2$\times$54 so floor length 54 has 108 purple tiles
$\therefore$ floor length 55 has 108 + 1 = 109 purple tiles
Floor length 55 has 55$^2$ = 3025 tiles
The sequence of odd-sided floors
Each odd-sided floor contains the last odd-sided floor in the middle, outlined in blue.




4 purple tiles are added each time
Side length 2 longer each time
109 = 1 + 4$\times$?
= 1 + 108
= 1 + 4$\times$27
So side length = 1 + 2$\times$27 = 55
$\therefore$ total number of tiles = 55$^2$ = 3025
Finding the number of rows
 There are 2 purple tiles on each row,
There are 2 purple tiles on each row,Except for the middle row which has 1 purple tile (on odd-sided floors)
109 tiles = 1 purple tile in the middle
+ 108 purple tiles in pairs
= 1 purple tile in the middle
+ 54 pairs on 54 rows
$\therefore$ there are 1 + 54 = 55 rows
So there are 55$^2$ = 3025 tiles
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...
Summing Consecutive Numbers
15 = 7 + 8 and 10 = 1 + 2 + 3 + 4. Can you say which numbers can be expressed as the sum of two or more consecutive integers?
1 Step 2 Step
Liam's house has a staircase with 12 steps. He can go down the steps one at a time or two at time. In how many different ways can Liam go down the 12 steps?

