Skip over navigation
Bill from Marshall Laing in New Zealand, and Neilesh from MPLS, both used a trial and improvement method to find the value of the dot when the number line showed 9 and 29. Bill said:
For the first one, the answer is 13 because I added 4 to 9, and then 4 again, and again, and I got up to 25, and the next one was 29.
Neliesh also found that:
0 would be between the 5th and 6th marks.
Oliver from The Priory Academy LSST in the UK, Hikari (Karin) from Bangkok Patana School in Thailand and Arnav from Franconian International School in Germany submitted a strategy for finding the dots. This is Oliver's work:
Method to find out the missing value:
1) Count how many intervals there are between the two given values.
2) Find the difference between the two values and divide that by the number of intervals.
3) Keep adding the result from the first value, until you reach the required missing value.
Eg:
_ _ _ _ _ 12 _ ? _ 60 _ _ _ _ _
In this example, there are 4 intervals between the 12 and 60. The difference between 12 and 60 is 48, so we divide 48 by 4. This gives us 12.
The missing value is two intervals ahead of 12, so we must add 12 two times. The answer, therefore, would be 36!
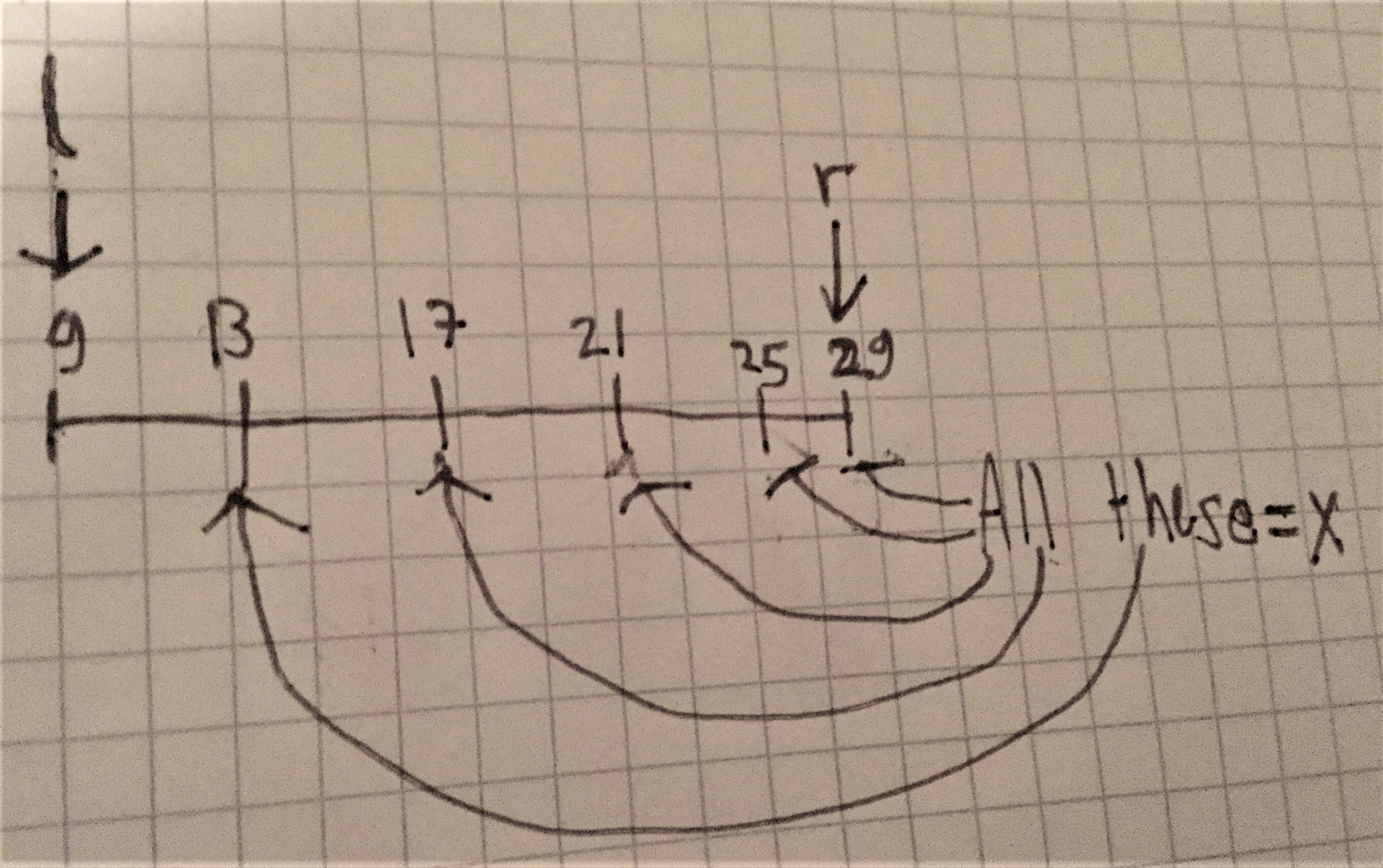
Arnav also included a formula to find the distance between each pair of lines, and a diagram:
If left number would $=l$,
and right number $= r$,
and number of lines from the furthest left number, to furthest right number $= x$,
then formula would be: $\dfrac{r-l}x$.
So, with the challenge that was given, the formula would be in that case:$\dfrac{29-9}5$
Solving:
$$\frac{29-9}5\\
=\dfrac{20}5\\
=4$$
This means that each line $=+4$
Number Lines in Disguise
Bill from Marshall Laing in New Zealand, and Neilesh from MPLS, both used a trial and improvement method to find the value of the dot when the number line showed 9 and 29. Bill said:
For the first one, the answer is 13 because I added 4 to 9, and then 4 again, and again, and I got up to 25, and the next one was 29.
Neliesh also found that:
0 would be between the 5th and 6th marks.
Oliver from The Priory Academy LSST in the UK, Hikari (Karin) from Bangkok Patana School in Thailand and Arnav from Franconian International School in Germany submitted a strategy for finding the dots. This is Oliver's work:
Method to find out the missing value:
1) Count how many intervals there are between the two given values.
2) Find the difference between the two values and divide that by the number of intervals.
3) Keep adding the result from the first value, until you reach the required missing value.
Eg:
_ _ _ _ _ 12 _ ? _ 60 _ _ _ _ _
In this example, there are 4 intervals between the 12 and 60. The difference between 12 and 60 is 48, so we divide 48 by 4. This gives us 12.
The missing value is two intervals ahead of 12, so we must add 12 two times. The answer, therefore, would be 36!
Arnav also included a formula to find the distance between each pair of lines, and a diagram:
If left number would $=l$,
and right number $= r$,
and number of lines from the furthest left number, to furthest right number $= x$,
then formula would be: $\dfrac{r-l}x$.
So, with the challenge that was given, the formula would be in that case:$\dfrac{29-9}5$
Solving:
$$\frac{29-9}5\\
=\dfrac{20}5\\
=4$$
This means that each line $=+4$
You may also like
Worms
Place this "worm" on the 100 square and find the total of the four squares it covers. Keeping its head in the same place, what other totals can you make?
Greetings
From a group of any 4 students in a class of 30, each has exchanged Christmas cards with the other three. Show that some students have exchanged cards with all the other students in the class. How many such students are there?
Writ Large
Suppose you had to begin the never ending task of writing out the natural numbers: 1, 2, 3, 4, 5.... and so on. What would be the 1000th digit you would write down.