Skip over navigation
If the small boxes are all packed in the same orientation, then the total number of boxes can be found by multiplying the number of boxes stacked along each edge. This is shown (with arbitrarily sized boxes) on the diagram below, where the large box contains 48 smaller boxes in this orientation:
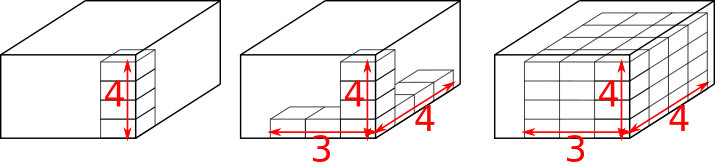
To choose the best orientation for the small boxes, we should consider how many small boxes would fit along each edge of the large box the different ways round. The less unused space, the better!
1.2 m = 120 cm, which is equal to:

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Packing Small Boxes
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
If the small boxes are all packed in the same orientation, then the total number of boxes can be found by multiplying the number of boxes stacked along each edge. This is shown (with arbitrarily sized boxes) on the diagram below, where the large box contains 48 smaller boxes in this orientation:

To choose the best orientation for the small boxes, we should consider how many small boxes would fit along each edge of the large box the different ways round. The less unused space, the better!
1.2 m = 120 cm, which is equal to:
- 8$\times$15, so this side could be made up of 8 boxes stacked along their 15 cm edges
- 6$\times$20, so it could also be 6 boxes stacked along their 20 cm edges
- 10$\times$15, so this could be 10 boxes stacked along their 15 cm edges
- 7$\times$20 + 10, so it could also be 20 boxes stacked along their 20 cm edges with 10 cm left over
- 8$\times$20 + 10 (8 boxes along their 20 cm edges, with 10 cm left over)
- 11$\times$15 + 5 (11 boxes along their 15 cm edges, with 5 cm left over)
- 10$\times$15 + 1$\times$20 (10 boxes along their 15 cm edges, and 1 box along its 20 cm edge)
- 7$\times$20 + 2$\times$15 (7 boxes along their 20 cm edges and 2 boxes along their 15 cm edges)
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Hallway Borders
What are the possible dimensions of a rectangular hallway if the number of tiles around the perimeter is exactly half the total number of tiles?

