Skip over navigation
Answer: $\dfrac{1}{\sqrt3-1} = \dfrac{1+\sqrt3}2 =1.366$ to 3 d.p.
Using the relationship between the areas
The area of the small square is $\frac13$ of the area of the large square, so $$\frac {x^2}{(x+y)^2}=\frac13\Rightarrow\left(\frac x{x+y}\right)^2=\frac13\Rightarrow\frac x{x+y}=\dfrac1{\sqrt3}$$
We can make $\dfrac x y$ the subject of this equation:
$$\begin{align}\frac{x}{x+y}&=\frac1{\sqrt3}\\
\Rightarrow\sqrt3x&=x+y\\
\Rightarrow\sqrt3x-x&=y\\
\Rightarrow(\sqrt3-1)x&=y\\
\Rightarrow\frac x y &=\frac 1 {\sqrt3-1}\end{align}$$
To see how to express this as a fraction with a whole number denominator, see the bottom of the solution.
Splitting the larger square into smaller squares and rectangles
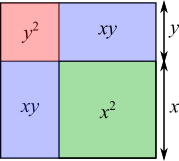 Green = $\frac13$ of total
Green = $\frac13$ of total
$\therefore$ red + blue = green $\times$ 2
$\Rightarrow y^2+2xy=2x^2$
$\Rightarrow 1+2\dfrac xy=2\dfrac{x^2}{y^2}$
Let $\dfrac xy=w$:
$$\begin{align}1+2w=2w^2&\Rightarrow 2w^2-2w-1=0\\
&\Rightarrow w^2-w-\tfrac12=0\\
&\Rightarrow\left(w-\tfrac12\right)^2-\tfrac14-\tfrac12=0\\
&\Rightarrow w-\tfrac12=\pm\tfrac{\sqrt3}{2}\\
&\Rightarrow w=\tfrac12\pm\tfrac{\sqrt3}{2}\text{ take the positive root since }w>0\\
&\Rightarrow w=\tfrac{1+\sqrt3}2\end{align}$$
Splitting the larger square into trapeziums
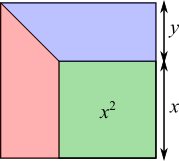 The area of each trapezium is $\frac12\left(\left(x+y\right)+x\right)y$
The area of each trapezium is $\frac12\left(\left(x+y\right)+x\right)y$
Green square occupies a third of the area
$\therefore$ the three shapes have equal area
$\frac12\left(\left(x+y\right)+x\right)y=x^2$
Multiplying both sides of this equation by $2$ and expanding gives $2xy+y^2=2x^2$.
$\dfrac xy$ can be found from this equation as shown above.
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
A Third of the Area
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Answer: $\dfrac{1}{\sqrt3-1} = \dfrac{1+\sqrt3}2 =1.366$ to 3 d.p.
Using the relationship between the areas
The area of the small square is $\frac13$ of the area of the large square, so $$\frac {x^2}{(x+y)^2}=\frac13\Rightarrow\left(\frac x{x+y}\right)^2=\frac13\Rightarrow\frac x{x+y}=\dfrac1{\sqrt3}$$
We can make $\dfrac x y$ the subject of this equation:
$$\begin{align}\frac{x}{x+y}&=\frac1{\sqrt3}\\
\Rightarrow\sqrt3x&=x+y\\
\Rightarrow\sqrt3x-x&=y\\
\Rightarrow(\sqrt3-1)x&=y\\
\Rightarrow\frac x y &=\frac 1 {\sqrt3-1}\end{align}$$
To see how to express this as a fraction with a whole number denominator, see the bottom of the solution.
Splitting the larger square into smaller squares and rectangles
 Green = $\frac13$ of total
Green = $\frac13$ of total$\therefore$ red + blue = green $\times$ 2
$\Rightarrow y^2+2xy=2x^2$
$\Rightarrow 1+2\dfrac xy=2\dfrac{x^2}{y^2}$
Let $\dfrac xy=w$:
$$\begin{align}1+2w=2w^2&\Rightarrow 2w^2-2w-1=0\\
&\Rightarrow w^2-w-\tfrac12=0\\
&\Rightarrow\left(w-\tfrac12\right)^2-\tfrac14-\tfrac12=0\\
&\Rightarrow w-\tfrac12=\pm\tfrac{\sqrt3}{2}\\
&\Rightarrow w=\tfrac12\pm\tfrac{\sqrt3}{2}\text{ take the positive root since }w>0\\
&\Rightarrow w=\tfrac{1+\sqrt3}2\end{align}$$
Splitting the larger square into trapeziums
 The area of each trapezium is $\frac12\left(\left(x+y\right)+x\right)y$
The area of each trapezium is $\frac12\left(\left(x+y\right)+x\right)y$Green square occupies a third of the area
$\therefore$ the three shapes have equal area
$\frac12\left(\left(x+y\right)+x\right)y=x^2$
Multiplying both sides of this equation by $2$ and expanding gives $2xy+y^2=2x^2$.
$\dfrac xy$ can be found from this equation as shown above.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Golden Thoughts
Rectangle PQRS has X and Y on the edges. Triangles PQY, YRX and XSP have equal areas. Prove X and Y divide the sides of PQRS in the golden ratio.
Two Cubes
Two cubes, each with integral side lengths, have a combined volume equal to the total of the lengths of their edges. How big are the cubes? [If you find a result by 'trial and error' you'll need to prove you have found all possible solutions.]
Square Mean
Is the mean of the squares of two numbers greater than, or less than, the square of their means?

