Skip over navigation
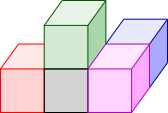
Colouring the cubes in different colours, as shown on the right, makes it easier to see what is happening.
Rotating the original shape
Keeping the same face at the front, which is in the shape of an upside-down T, and rotating clockwise, we get the shapes below:
Rotation 1 Rotation 2

 Rotation 1 looks like shape D, but they are not the same. So shape D is not possible keeping this face at the front.
Rotation 1 looks like shape D, but they are not the same. So shape D is not possible keeping this face at the front.
Rotation 1 Shape D

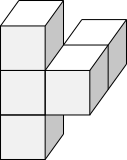
Rotation 2 looks like shape A and shape C.
Shape A Rotation 2 Shape C
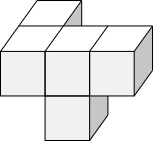

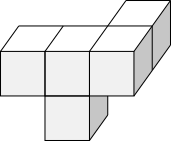
In fact, it is exactly the same as shape A, so shape A is possible. But it is not the same as shape C so shape C is not possible with this face at the front.
Shape B has the front T face in the same orientation as the original, but it is not the same. So with this face at the front, it is not possible to obtain shape B.
To check whether putting a different face at the front will help, we can rotate the original shape so that other faces are at the front. To reach any of shapes B, C or D, it will be necessary for the front face to look like a rotated T.
Keeping the pink cube on the right and rotating forwards gives:
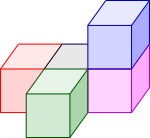

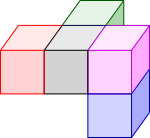
And keeping the green cube on the top and rotating clockwise gives:
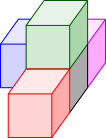

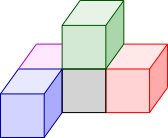
None of the resulting front faces is a T shape, so shapes B, C and D are impossible.
 Colouring the possibilities
Colouring the possibilities
The coloured original is shown again on the right.
Notice that the dark grey cube is the only cube that shares faces with 3 other cubes - this means we should be able to find it on shapes A, B, C and D if they are possible rotations. It is shaded below.
Shape A Shape B Shape C Shape D
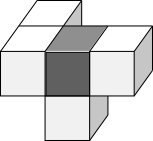
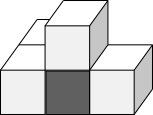
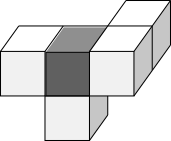
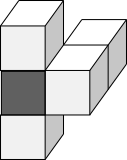
Then, of the 3 cubes which share a face with the grey cube, only the pink cube shares a face with another cube. So it can be found on shapes A, B and C, but does not exist on shape D. So shape D is not a rotation of the original shape.
Shape A Shape B Shape C

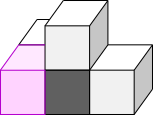

The other cube touching the pink cube is the blue cube.
Below, purple and yellow dots have been added to a pair of vertices on each shape. They are on the two vertices of the pink cube that don't touch the grey or blue cubes. This is the same for all of the cubes. The yellow dot is always closer to the green cube than the purple dot.
Original Shape A Shape B Shape C
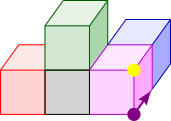
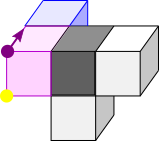

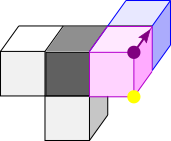
Imagine a person standing with their feet on the purple dot, facing towards the blue cube (so looking along the purple arrow), and their head on the yellow dot.
This person would be rotated with the shape, so the shape would still look the same to them.
Is the grey cube on their left or on their right?
Original - on their left
Shape A - on their left
Shape B - on their right
Shape D - on their right
So only shape A can be reached by rotation.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Rotation Identification
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions

Colouring the cubes in different colours, as shown on the right, makes it easier to see what is happening.
Rotating the original shape
Keeping the same face at the front, which is in the shape of an upside-down T, and rotating clockwise, we get the shapes below:
Rotation 1 Rotation 2


Rotation 1 Shape D


Rotation 2 looks like shape A and shape C.
Shape A Rotation 2 Shape C



In fact, it is exactly the same as shape A, so shape A is possible. But it is not the same as shape C so shape C is not possible with this face at the front.
Shape B has the front T face in the same orientation as the original, but it is not the same. So with this face at the front, it is not possible to obtain shape B.
To check whether putting a different face at the front will help, we can rotate the original shape so that other faces are at the front. To reach any of shapes B, C or D, it will be necessary for the front face to look like a rotated T.
Keeping the pink cube on the right and rotating forwards gives:



And keeping the green cube on the top and rotating clockwise gives:



None of the resulting front faces is a T shape, so shapes B, C and D are impossible.
 Colouring the possibilities
Colouring the possibilitiesThe coloured original is shown again on the right.
Notice that the dark grey cube is the only cube that shares faces with 3 other cubes - this means we should be able to find it on shapes A, B, C and D if they are possible rotations. It is shaded below.
Shape A Shape B Shape C Shape D




Then, of the 3 cubes which share a face with the grey cube, only the pink cube shares a face with another cube. So it can be found on shapes A, B and C, but does not exist on shape D. So shape D is not a rotation of the original shape.
Shape A Shape B Shape C

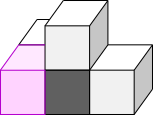

The other cube touching the pink cube is the blue cube.
Below, purple and yellow dots have been added to a pair of vertices on each shape. They are on the two vertices of the pink cube that don't touch the grey or blue cubes. This is the same for all of the cubes. The yellow dot is always closer to the green cube than the purple dot.
Original Shape A Shape B Shape C




Imagine a person standing with their feet on the purple dot, facing towards the blue cube (so looking along the purple arrow), and their head on the yellow dot.
This person would be rotated with the shape, so the shape would still look the same to them.
Is the grey cube on their left or on their right?
Original - on their left
Shape A - on their left
Shape B - on their right
Shape D - on their right
So only shape A can be reached by rotation.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...

