Skip over navigation
Lewis from Dartford Grammar School for Boys in the UK, Dang Minh Duc from Renaissance International School Saigon in Vietnam, Alex from Chorlton High School in the UK and Anas all proved Alison's conjecture using the interior angles in a triangle. This is Dang Minh Duc's work:
b + x = 90$^\circ$
g + y = 90$^\circ$
b + g + y + x = 180$^\circ$ (from adding the above equations)
r + x + y = 180$^\circ$ (because angles in a triangle add up to 180$^\circ$)
b + g + y + x = r + y + x
b + g = r
Alternatively, Alex and Lewis expressed x and y in terms of b and g:
x = 90$^\circ - $b, y = 90$^\circ - $g, so r + (90$^\circ - $b) + (90$^\circ - $g) = 180$^\circ$
so 180$^\circ$ = 180$^\circ$ + r$- $g$-$b, so r$- $g$-$b = 0, so r = g + b
Leah, Hazel, Kaitlyn, Hollie and Sofia from Ormiston Ilkeston Enterprise Academy, Lewis from Dartford Grammar School for Boys, Alex from Chorlton High School, Baruch from Westminster School, William from The Hurst Community College (all in the UK), Anas, Daniel from Seoul Foreign British School and Thomas from Hollinwood Academy in the UK proved the conjecture using alternate angles. This is Daniel's diagram and Thomas' explanation:
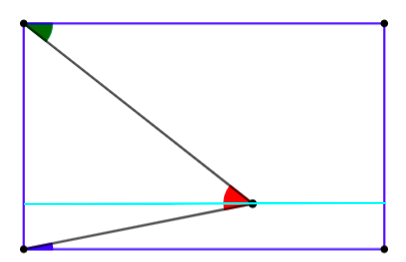
The angle in the top left (green) must be equal to the top portion of the created angle (red angle above the blue line) and the same with the bottom left angle (blue) and the bottom part of the created angle (red angle below the blue line). Thus when you add the two angles up, you get the created angle (red) all by the alternate angles rule!
(or 'Z' angles)
William from The Hurst Community College in the UK used a vertical line to form right-angled triangles:
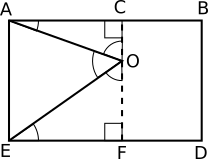
$A\hat{O}C = 90^\circ - O\hat A C$
$E\hat{O}F = 90^\circ - O\hat{E}F$
$E\hat{O}A = 180^\circ - A\hat{O}C-E\hat{O}F$
$\therefore E\hat{O}A=180^\circ - \left(90^\circ - O\hat{A}C\right) - \left(90^\circ-O\hat{E}F\right)$
$E\hat{O}A=O\hat{A}C + O\hat{E}F$
Lewis from Dartford Grammar School for Boys in the UK also proved it using a pentagon:
Sum of interior angles in a pentagon:
Each angle between two perpendicular sides, by definition is 90 °. Therefore, we know 2 of the angles in the pentagon are each 90 °.
Reflex on opposite side of point where r is located
= 360 ° $-$ r
540 ° = 180 ° + g + b + 360 $-$ r
0 = g + b $-$ r
r = g + b
Parallelogram and Trapezium
Lewis, Baruch and Anas used the interior angles of a triangle to prove that this also works for parallelograms and trapeziums. The proof is very similar to the proof for rectangles. This is Lewis' working with a diagram added:
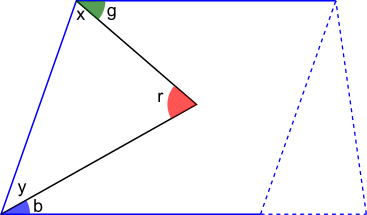1) Co-interior angles sum to 180 °
((g + x) + (b + y))
2) The base angles in the triangle sum to 180 ° $-$ g $-$ b
(x + y)
3) The sum of angles in a triangle = 180 °
4) 180 ° = 180 ° $-$ g $-$ b + r
0 = r $-$ g $-$ b
r = g + b
William and Anas also proved these cases using alternate angles. These are William's diagrams:
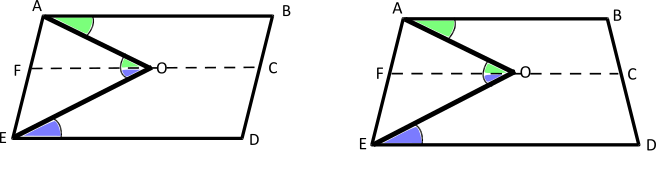
William and also used a method using right-angled triangles:
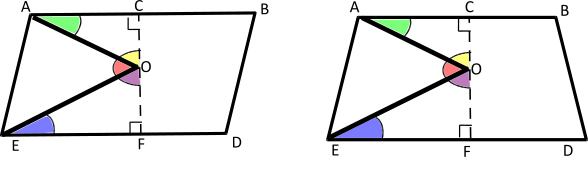
The yellow and green angles add up to 90$^\circ$
The blue and purple angles add up to 90$^\circ$
So yellow + green + blue + purple = 180$^\circ$
But yellow + red + purple = 180$^\circ$
So green + blue = red.
Baruch thought about what happens when the point is outside the rectangle, and claimed that the alternate angles proof would still work:
If the point goes outside the rectangle, the same theory applies. The “extended” dotted line would still be parallel to AD and CE, so the red angle would still maintain its composition as the sum of the green angle and the blue angle)
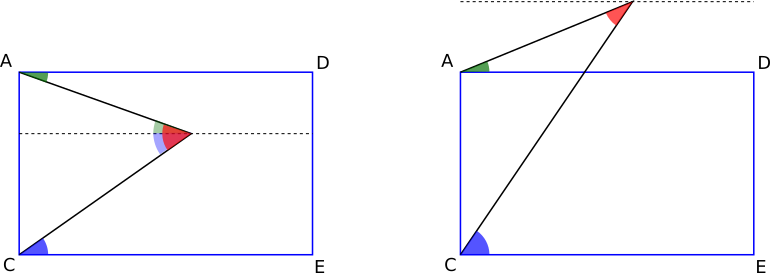
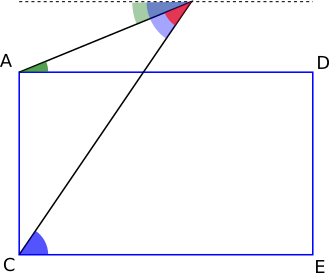
However, a closer look at which angles are the alternate angles in this case shows that actually, the red angle is now the difference between the blue and green angles (unless the green angle is now considered 'negative'):
Angles Inside
Age 11 to 14
Challenge Level 
Lewis from Dartford Grammar School for Boys in the UK, Dang Minh Duc from Renaissance International School Saigon in Vietnam, Alex from Chorlton High School in the UK and Anas all proved Alison's conjecture using the interior angles in a triangle. This is Dang Minh Duc's work:
b + x = 90$^\circ$
g + y = 90$^\circ$
b + g + y + x = 180$^\circ$ (from adding the above equations)
r + x + y = 180$^\circ$ (because angles in a triangle add up to 180$^\circ$)
b + g + y + x = r + y + x
b + g = r
Alternatively, Alex and Lewis expressed x and y in terms of b and g:
x = 90$^\circ - $b, y = 90$^\circ - $g, so r + (90$^\circ - $b) + (90$^\circ - $g) = 180$^\circ$
so 180$^\circ$ = 180$^\circ$ + r$- $g$-$b, so r$- $g$-$b = 0, so r = g + b
Leah, Hazel, Kaitlyn, Hollie and Sofia from Ormiston Ilkeston Enterprise Academy, Lewis from Dartford Grammar School for Boys, Alex from Chorlton High School, Baruch from Westminster School, William from The Hurst Community College (all in the UK), Anas, Daniel from Seoul Foreign British School and Thomas from Hollinwood Academy in the UK proved the conjecture using alternate angles. This is Daniel's diagram and Thomas' explanation:
The angle in the top left (green) must be equal to the top portion of the created angle (red angle above the blue line) and the same with the bottom left angle (blue) and the bottom part of the created angle (red angle below the blue line). Thus when you add the two angles up, you get the created angle (red) all by the alternate angles rule!
(or 'Z' angles)
William from The Hurst Community College in the UK used a vertical line to form right-angled triangles:
$A\hat{O}C = 90^\circ - O\hat A C$
$E\hat{O}F = 90^\circ - O\hat{E}F$
$E\hat{O}A = 180^\circ - A\hat{O}C-E\hat{O}F$
$\therefore E\hat{O}A=180^\circ - \left(90^\circ - O\hat{A}C\right) - \left(90^\circ-O\hat{E}F\right)$
$E\hat{O}A=O\hat{A}C + O\hat{E}F$
Lewis from Dartford Grammar School for Boys in the UK also proved it using a pentagon:
Sum of interior angles in a pentagon:
180 °(n$-$2) = sum
180 ° (5$-$2) = sum
180 °$\times$3 = 540 °
180 ° (5$-$2) = sum
180 °$\times$3 = 540 °
Each angle between two perpendicular sides, by definition is 90 °. Therefore, we know 2 of the angles in the pentagon are each 90 °.
Reflex on opposite side of point where r is located
= 360 ° $-$ r
540 ° = 180 ° + g + b + 360 $-$ r
0 = g + b $-$ r
r = g + b
Parallelogram and Trapezium
Lewis, Baruch and Anas used the interior angles of a triangle to prove that this also works for parallelograms and trapeziums. The proof is very similar to the proof for rectangles. This is Lewis' working with a diagram added:
1) Co-interior angles sum to 180 °((g + x) + (b + y))
2) The base angles in the triangle sum to 180 ° $-$ g $-$ b
(x + y)
3) The sum of angles in a triangle = 180 °
4) 180 ° = 180 ° $-$ g $-$ b + r
0 = r $-$ g $-$ b
r = g + b
William and Anas also proved these cases using alternate angles. These are William's diagrams:
William and also used a method using right-angled triangles:
The yellow and green angles add up to 90$^\circ$
The blue and purple angles add up to 90$^\circ$
So yellow + green + blue + purple = 180$^\circ$
But yellow + red + purple = 180$^\circ$
So green + blue = red.
Baruch thought about what happens when the point is outside the rectangle, and claimed that the alternate angles proof would still work:
If the point goes outside the rectangle, the same theory applies. The “extended” dotted line would still be parallel to AD and CE, so the red angle would still maintain its composition as the sum of the green angle and the blue angle)
However, a closer look at which angles are the alternate angles in this case shows that actually, the red angle is now the difference between the blue and green angles (unless the green angle is now considered 'negative'):
You may also like
Arclets Explained
This article gives an wonderful insight into students working on the Arclets problem that first appeared in the Sept 2002 edition of the NRICH website.
Bow Tie
Show how this pentagonal tile can be used to tile the plane and describe the transformations which map this pentagon to its images in the tiling.