Skip over navigation
Drawing more little triangles
The length DE, which is the base of the triangle, fits 4 times along the side DC. So 4 copies of the triangle fit with their bases along DC:
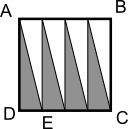
The white unshaded triangles are congruent to the grey shaded triangles, so they have the same area. There are 4 shaded triangles and 4 unshaded triangles, so there are 8 triangles altogether.
So the area of each triangle is $\frac18$ of the area of the square.
Finding the area of the square and the triangle
Suppose the square has side length $1$, so that its area is $1$. We can do this because we don't need to know what the area of the triangle is as a number, we just want to know it as a fraction of the area of the square. And finding numbers as fractions of $1$ is easy - for example, $\frac12$ of $1$ is just $\frac12$.
Then the height of the triangle is $1$, since it is the side length of the square.
$4\times=1$. So the length DE, which is the base of the triangle, is $\frac14$
So the area of the triangle is $\frac12\times\frac14\times1=\frac12\times\frac14=\frac18$
And $\frac18$ as a fraction of $1$ is just $\frac18$. So the area of the triangle is $\frac18$ of the area of the square.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Fraction of a Square
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
Drawing more little triangles
The length DE, which is the base of the triangle, fits 4 times along the side DC. So 4 copies of the triangle fit with their bases along DC:

The white unshaded triangles are congruent to the grey shaded triangles, so they have the same area. There are 4 shaded triangles and 4 unshaded triangles, so there are 8 triangles altogether.
So the area of each triangle is $\frac18$ of the area of the square.
Finding the area of the square and the triangle
Suppose the square has side length $1$, so that its area is $1$. We can do this because we don't need to know what the area of the triangle is as a number, we just want to know it as a fraction of the area of the square. And finding numbers as fractions of $1$ is easy - for example, $\frac12$ of $1$ is just $\frac12$.
Then the height of the triangle is $1$, since it is the side length of the square.
$4\times=1$. So the length DE, which is the base of the triangle, is $\frac14$
So the area of the triangle is $\frac12\times\frac14\times1=\frac12\times\frac14=\frac18$
And $\frac18$ as a fraction of $1$ is just $\frac18$. So the area of the triangle is $\frac18$ of the area of the square.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...

