Skip over navigation
Answer: $30\%$
Using ratio and parts
$450$ and $630$ are in the ratio $45:63 = 5:7$
$$
\begin{array}
\text{5 parts 42%} \\
\text{7 parts ?%}
\end{array}
\bigg\}
\text{12 parts 35%}$$
Working backwards from the new juice,
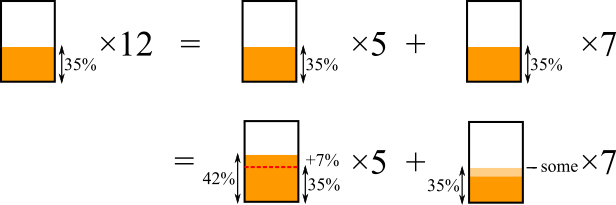
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad+7\%\times5$ balances with $-\text{some}\times7$
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\Rightarrow 35\%=\text{some}\times7$
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\Rightarrow \text{some}=5\%$
$35\%-5\%=30\%\therefore$ the orange drink was 30% juice.
Finding the amounts of juice
$450 + 630 = 1080$
$42\%$ of $450 =42\%$ of $100\times4.5=42\times4.5 = 189$
$35\%$ of $1080= 35\%$ of $1000 + 35\%$ of $80$, which is $350 + 24 + 4 = 378$
$378-189=189 \therefore 189$ litres of juice comes from $630$ litres orange drink
$\dfrac{189}{630}=\dfrac{63}{210}=\dfrac{21}{70}=\dfrac{3}{10}=30\%$
Using ratio and total juice
$450$ and $630$ are in the ratio $45:63 = 5:7$
$$
\begin{array}
\text{5 parts 42%} \\
\text{7 parts ?%}
\end{array}
\bigg\}
\text{12 parts 35%}$$
Since we are working in 'parts' and not specific units, we can simply multiply by 42 and 35, instead of finding 42% and 35%, because 42% and 35% are in the same ratio as 42 and 35.
$42\times5 + ?\times7 = 35\times12$
$\Rightarrow7\times6\times5 + 7\times? = 7\times5\times12$
$\Rightarrow7\times(6\times5 + ?) = 7\times5\times12$
$\Rightarrow6\times5 + ? = 5\times12$
$\Rightarrow30 + ? = 60$
$\Rightarrow? = 30$
Using fractions
450 and 630 are in the ratio 45:63 = 5:7, so the mixture is $\frac5{12}$ pineapple drink and $\frac7{12}$ orange drink.
So we know that 42% of $\frac5{12}$ of the mixture is juice and that 35% of the whole mixture is juice. Let $x$ be the fraction of the orange drink that is juice. Then:
$$\begin{align}
\frac{42}{100}\times\frac5{12}\hspace{6mm}+\hspace{5mm}x\times\frac{7}{12}&=\hspace{3mm}\frac{35}{100}&\\
\Rightarrow \frac{6\times7}{20\times5}\times\frac{5}{6\times2}\hspace{1mm}+\hspace{5mm}x\times\frac7{12}&=\frac{7\times5}{20\times5}\\
\Rightarrow \frac7{20\times2}\hspace{8mm}+\hspace{5mm}x\times\frac7{12}&=\hspace{3mm}\frac{7}{20}\\
\Rightarrow x\times\frac7{12}&=\frac{7\times2}{20\times2}-\frac7{20\times2}\\
\Rightarrow x\times\frac7{6\times2}&=\frac{7}{20\times2}\\
\Rightarrow x\times\frac16&=\frac1{20}\\
\Rightarrow x&=\frac6{20}\\
\Rightarrow x&=\frac3{10}
\end{align}$$ Which is the same as 30%.



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Pineapple Juice
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Answer: $30\%$
Using ratio and parts
$450$ and $630$ are in the ratio $45:63 = 5:7$
$$
\begin{array}
\text{5 parts 42%} \\
\text{7 parts ?%}
\end{array}
\bigg\}
\text{12 parts 35%}$$
Working backwards from the new juice,

$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad+7\%\times5$ balances with $-\text{some}\times7$
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\Rightarrow 35\%=\text{some}\times7$
$\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\Rightarrow \text{some}=5\%$
$35\%-5\%=30\%\therefore$ the orange drink was 30% juice.
Finding the amounts of juice
$450 + 630 = 1080$
$42\%$ of $450 =42\%$ of $100\times4.5=42\times4.5 = 189$
$35\%$ of $1080= 35\%$ of $1000 + 35\%$ of $80$, which is $350 + 24 + 4 = 378$
$378-189=189 \therefore 189$ litres of juice comes from $630$ litres orange drink
$\dfrac{189}{630}=\dfrac{63}{210}=\dfrac{21}{70}=\dfrac{3}{10}=30\%$
Using ratio and total juice
$450$ and $630$ are in the ratio $45:63 = 5:7$
$$
\begin{array}
\text{5 parts 42%} \\
\text{7 parts ?%}
\end{array}
\bigg\}
\text{12 parts 35%}$$
Since we are working in 'parts' and not specific units, we can simply multiply by 42 and 35, instead of finding 42% and 35%, because 42% and 35% are in the same ratio as 42 and 35.
$42\times5 + ?\times7 = 35\times12$
$\Rightarrow7\times6\times5 + 7\times? = 7\times5\times12$
$\Rightarrow7\times(6\times5 + ?) = 7\times5\times12$
$\Rightarrow6\times5 + ? = 5\times12$
$\Rightarrow30 + ? = 60$
$\Rightarrow? = 30$
Using fractions
450 and 630 are in the ratio 45:63 = 5:7, so the mixture is $\frac5{12}$ pineapple drink and $\frac7{12}$ orange drink.
So we know that 42% of $\frac5{12}$ of the mixture is juice and that 35% of the whole mixture is juice. Let $x$ be the fraction of the orange drink that is juice. Then:
$$\begin{align}
\frac{42}{100}\times\frac5{12}\hspace{6mm}+\hspace{5mm}x\times\frac{7}{12}&=\hspace{3mm}\frac{35}{100}&\\
\Rightarrow \frac{6\times7}{20\times5}\times\frac{5}{6\times2}\hspace{1mm}+\hspace{5mm}x\times\frac7{12}&=\frac{7\times5}{20\times5}\\
\Rightarrow \frac7{20\times2}\hspace{8mm}+\hspace{5mm}x\times\frac7{12}&=\hspace{3mm}\frac{7}{20}\\
\Rightarrow x\times\frac7{12}&=\frac{7\times2}{20\times2}-\frac7{20\times2}\\
\Rightarrow x\times\frac7{6\times2}&=\frac{7}{20\times2}\\
\Rightarrow x\times\frac16&=\frac1{20}\\
\Rightarrow x&=\frac6{20}\\
\Rightarrow x&=\frac3{10}
\end{align}$$ Which is the same as 30%.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like

Percentage Unchanged
If the base of a rectangle is increased by 10% and the area is unchanged, by what percentage is the width decreased by ?
Circle Packing
Equal circles can be arranged so that each circle touches four or six others. What percentage of the plane is covered by circles in each packing pattern? ...
Round and Round
Prove that the shaded area of the semicircle is equal to the area of the inner circle.

