Skip over navigation
Using three-way scale factors
Compared to the 50 m rope, the 100 m rope is twice as long, and the diameter of the cross-section is 11 rather than 9, which is an increase by a scale factor of $\frac{11}9$.
We can create this by enlarging the 50 m rope in 3 different directions, which are all perpendicular to each other, as shown in this diagram:
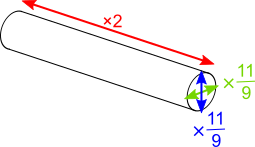
The weight of the 50 m rope is approximately 2.7 kg, so the weight (in kg) of the 100 m rope is approximately $2.7\times2\times\frac{11}9\times\frac{11}9=2.7\times2\times\frac{121}{81}$
$\frac{121}{81}\approx\frac{120}{80}=\frac32$, so the weight of the 10 m rope is approximately $2.7\times2\times\frac32=2.7\times3=8.1$ kg.
Notice that equivalently, increasing the diameter, a length, by a scale factor of $\frac{11}9$ (without changing the shape of the cross-section) has the effect of increasing the area by a scale factor of $\left(\frac{11}9\right)^2$.
Using formulae
The area of the cross-section of the 50 m rope is $\pi \left(\frac92\right)^2$ square millimetres, and its length is $50000$ mm. So its volume is $50000\times\pi\times\left(\frac92\right)^2$, which means that $50000\times\pi\times\left(\frac92\right)^2\times d=2.7$, where $d$ is the weight of each cubic millimetre of the material the rope is made from (its density).
The 100 m rope is $100 000$ mm long with a cross-sectional area of $\pi \left(\frac{11}2\right)^2$ square millimetres, so its weight will be $100000\times\pi\times\left(\frac92\right)^2\times d$
We can rewrite these to compare them:
50 m rope: $50 000\times \pi \times 9^2 \div 2^2 = 2.7$
100 m rope: $(2\times50 000)\times\pi \times 11^2\div 2^2 = \hspace{1mm} ?$
So to get from the weight of the 50 m rope to the weight of the 100 m rope, we need to multiply by $2$, divide by $9^2$ and multiply by $11^2$. So the weight of the 100 m rope is approximately: $2.7\times2\times121\div81\approx 2.7\times 2\times (120\div 80)=2.7\times2\times\frac32=2.7\times3=8.1$ kg
Climbing Ropes
Age 14 to 16
ShortChallenge Level 
Using three-way scale factors
Compared to the 50 m rope, the 100 m rope is twice as long, and the diameter of the cross-section is 11 rather than 9, which is an increase by a scale factor of $\frac{11}9$.
We can create this by enlarging the 50 m rope in 3 different directions, which are all perpendicular to each other, as shown in this diagram:
The weight of the 50 m rope is approximately 2.7 kg, so the weight (in kg) of the 100 m rope is approximately $2.7\times2\times\frac{11}9\times\frac{11}9=2.7\times2\times\frac{121}{81}$
$\frac{121}{81}\approx\frac{120}{80}=\frac32$, so the weight of the 10 m rope is approximately $2.7\times2\times\frac32=2.7\times3=8.1$ kg.
Notice that equivalently, increasing the diameter, a length, by a scale factor of $\frac{11}9$ (without changing the shape of the cross-section) has the effect of increasing the area by a scale factor of $\left(\frac{11}9\right)^2$.
Using formulae
The area of the cross-section of the 50 m rope is $\pi \left(\frac92\right)^2$ square millimetres, and its length is $50000$ mm. So its volume is $50000\times\pi\times\left(\frac92\right)^2$, which means that $50000\times\pi\times\left(\frac92\right)^2\times d=2.7$, where $d$ is the weight of each cubic millimetre of the material the rope is made from (its density).
The 100 m rope is $100 000$ mm long with a cross-sectional area of $\pi \left(\frac{11}2\right)^2$ square millimetres, so its weight will be $100000\times\pi\times\left(\frac92\right)^2\times d$
We can rewrite these to compare them:
50 m rope: $50 000\times \pi \times 9^2 \div 2^2 = 2.7$
100 m rope: $(2\times50 000)\times\pi \times 11^2\div 2^2 = \hspace{1mm} ?$
So to get from the weight of the 50 m rope to the weight of the 100 m rope, we need to multiply by $2$, divide by $9^2$ and multiply by $11^2$. So the weight of the 100 m rope is approximately: $2.7\times2\times121\div81\approx 2.7\times 2\times (120\div 80)=2.7\times2\times\frac32=2.7\times3=8.1$ kg
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Some(?) of the Parts
A circle touches the lines OA, OB and AB where OA and OB are perpendicular. Show that the diameter of the circle is equal to the perimeter of the triangle
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
Bendy Quad
Four rods are hinged at their ends to form a convex quadrilateral. Investigate the different shapes that the quadrilateral can take. Be patient this problem may be slow to load.