Skip over navigation
Answer: $\frac19$
Finding the distance
The distance between $\frac16$ and $\frac1{12}$ is $\frac16-\frac1{12}=\frac{2}{12}-\frac1{12}=\frac1{12}$
Length of each of the 3 sections is equal to $\frac13$ of $\frac1{12}=\frac1{36}$
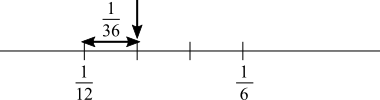
So the number indicated is $\frac1{12}+\frac1{36}=\frac3{36}+\frac1{36}=\frac4{36}=\frac19$
Using a weighted average
To find the point half way between $\frac16$ and $\frac1{12}$, we would add $\frac16$ and $\frac1{12}$ and divide by $2.$
We want the point that is twice as close to $\frac1{12}$ as it is to $\frac16$ - so give twice as much importance to $\frac1{12}$ as to $\frac16.$ This is called a weighted average.
$$\begin{split}\left(\tfrac16+2\times\tfrac1{12}\right)\div3&=\left(\tfrac16+\tfrac16\right)\div3\\
&=\tfrac26\div3\\&=\tfrac13\div3\\&=\tfrac19\end{split}$$


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Between a Sixth and a Twelfth
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
Answer: $\frac19$
Finding the distance
The distance between $\frac16$ and $\frac1{12}$ is $\frac16-\frac1{12}=\frac{2}{12}-\frac1{12}=\frac1{12}$
Length of each of the 3 sections is equal to $\frac13$ of $\frac1{12}=\frac1{36}$
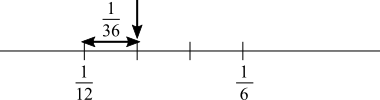
So the number indicated is $\frac1{12}+\frac1{36}=\frac3{36}+\frac1{36}=\frac4{36}=\frac19$
Using a weighted average
To find the point half way between $\frac16$ and $\frac1{12}$, we would add $\frac16$ and $\frac1{12}$ and divide by $2.$
We want the point that is twice as close to $\frac1{12}$ as it is to $\frac16$ - so give twice as much importance to $\frac1{12}$ as to $\frac16.$ This is called a weighted average.
$$\begin{split}\left(\tfrac16+2\times\tfrac1{12}\right)\div3&=\left(\tfrac16+\tfrac16\right)\div3\\
&=\tfrac26\div3\\&=\tfrac13\div3\\&=\tfrac19\end{split}$$
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...

