Skip over navigation
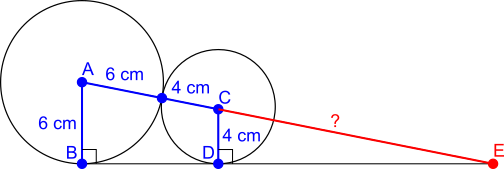
The radii of the circles along the side of the triangle are also shown in the diagram below.
Using the similar triangles in the diagram
Triangles AEB and CED are similar. The scale factor from CED to AEB is the same as the scale factor from CD to AB, ie from 4 cm to 6 cm.
This is the same as adding half of the original length.
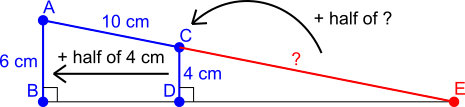
So to find the length AE from the length CE, you would need to add half of the length CE.
But the length you need to add is AC, which is 10 cm.
So CE must be 20 cm.
Drawing a line to make another similar triangle
6 cm can be split into 4 cm and 2 cm.
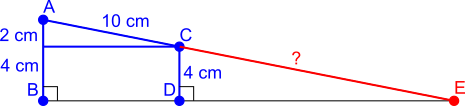
The triangle with sides 2 cm and 10 cm is similar to the triangle with sides 4 cm and ?.
So the ratios 2 : 10 and 4 : ? are the same.
So ? = 20 cm.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Circles on a Triangle
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
The radii of the circles along the side of the triangle are also shown in the diagram below.

Using the similar triangles in the diagram
Triangles AEB and CED are similar. The scale factor from CED to AEB is the same as the scale factor from CD to AB, ie from 4 cm to 6 cm.
This is the same as adding half of the original length.

So to find the length AE from the length CE, you would need to add half of the length CE.
But the length you need to add is AC, which is 10 cm.
So CE must be 20 cm.
Drawing a line to make another similar triangle
6 cm can be split into 4 cm and 2 cm.

The triangle with sides 2 cm and 10 cm is similar to the triangle with sides 4 cm and ?.
So the ratios 2 : 10 and 4 : ? are the same.
So ? = 20 cm.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Some(?) of the Parts
A circle touches the lines OA, OB and AB where OA and OB are perpendicular. Show that the diameter of the circle is equal to the perimeter of the triangle
Triangle Midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?
Fermat's Poser
Find the point whose sum of distances from the vertices (corners) of a given triangle is a minimum.

