Skip over navigation
It is helpful to draw a simple diagram of the situation.
We assume that the cat's eye is at the same height as the top of the wall. The blue line show's the cat's line of vision as it looks over the bush at the tree.
Consider the pink triangles on the diagram below. Their sloped sides are along the same straight line (the blue line). So they both have the same slope, or gradient - and make the same angle with the bases of the triangles.
They also have the same base, H metres, and are both right-angled.
So they share a base and the two angles on either sides of it - which means that they are congruent.
The tree is 3 metres taller than the bush, so the vertical side of the pink triangle between the bush and the tree is 3 metres.
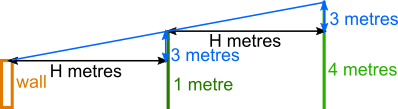
That means that the vertical side of the triangle between the wall and the bush is also 3 metres.
So, since the bush is 4 metres tall, the wall must be only 1 metre high.
Cat on a Wall
Age 14 to 16
ShortChallenge Level 
It is helpful to draw a simple diagram of the situation.
We assume that the cat's eye is at the same height as the top of the wall. The blue line show's the cat's line of vision as it looks over the bush at the tree.
Consider the pink triangles on the diagram below. Their sloped sides are along the same straight line (the blue line). So they both have the same slope, or gradient - and make the same angle with the bases of the triangles.
They also have the same base, H metres, and are both right-angled.So they share a base and the two angles on either sides of it - which means that they are congruent.
The tree is 3 metres taller than the bush, so the vertical side of the pink triangle between the bush and the tree is 3 metres.
That means that the vertical side of the triangle between the wall and the bush is also 3 metres.
So, since the bush is 4 metres tall, the wall must be only 1 metre high.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Some(?) of the Parts
A circle touches the lines OA, OB and AB where OA and OB are perpendicular. Show that the diameter of the circle is equal to the perimeter of the triangle
Triangle Midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?
Fermat's Poser
Find the point whose sum of distances from the vertices (corners) of a given triangle is a minimum.