Skip over navigation
Answer: 9
Suppose the width is $w$, then the length is $w+16$.
The area is equal to the product of the length and the width:
Area is $w\times(w+16) = 225$.
So the length and the width are a factor pair of 225.
225 = 5 $\times$ 5 $\times$ 3 $\times$ 3
225 = 5 $\times$ 45, difference = 40
225 = 15 $\times$ 15, difference = 0
225 = 9 $\times$ 25, difference = 16
$\therefore$ width = 9
Using trial & improvement
We can try different numbers for $w$ (knowing that it is 16 less than the length):
If $w=1$, then the area would be $1\times 17=17$ - too small.
If $w=20$, then the area would be $20\times 36=720$ - too big.
If $w=5$, then the area would be $5\times 21=105$ - too small.
If $w=10$, then the area would be $10\times 26=260$ - just too big.
If $w=9$, then the area would be $9\times 25=225$ - perfect.
So $w=9$.
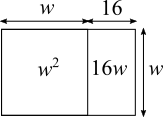 Using algebra
Using algebra
Area $w^2+16w=225$
Completing the square
$(w+8)^2=w^2+8w+8w+64=(w^2+16w)+64$
So $(w+8)^2-64 = w^2+16w\\
\begin{align}\therefore w^2+16w=225&\Rightarrow(w+8)^2-64 =225\\
&\Rightarrow (w+8)^2=289\\
&\Rightarrow (w+8)=\pm17\\
&\Rightarrow w=\pm17 - 8\end{align}$
$w$ must be positive, so $w=17-8=9$.
Using the quadratic formula
$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$
$w$ is the variable $x$, and $a=1$, $b=16$, $c=-225$
$\begin{align}w&=\dfrac{-16\pm\sqrt{16^2+4\times225}}{2}\\
&=-8\pm\sqrt{16\times4+225}\\
&=-8\pm\sqrt{289}\\
&=-8\pm17\end{align}$
Need width to be positive so $w=-8+17=9$


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Length, Width and Area
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Answer: 9
Suppose the width is $w$, then the length is $w+16$.
The area is equal to the product of the length and the width:
Area is $w\times(w+16) = 225$.
So the length and the width are a factor pair of 225.
225 = 5 $\times$ 5 $\times$ 3 $\times$ 3
225 = 5 $\times$ 45, difference = 40
225 = 15 $\times$ 15, difference = 0
225 = 9 $\times$ 25, difference = 16
$\therefore$ width = 9
Using trial & improvement
We can try different numbers for $w$ (knowing that it is 16 less than the length):
If $w=1$, then the area would be $1\times 17=17$ - too small.
If $w=20$, then the area would be $20\times 36=720$ - too big.
If $w=5$, then the area would be $5\times 21=105$ - too small.
If $w=10$, then the area would be $10\times 26=260$ - just too big.
If $w=9$, then the area would be $9\times 25=225$ - perfect.
So $w=9$.
 Using algebra
Using algebraArea $w^2+16w=225$
Completing the square
$(w+8)^2=w^2+8w+8w+64=(w^2+16w)+64$
So $(w+8)^2-64 = w^2+16w\\
\begin{align}\therefore w^2+16w=225&\Rightarrow(w+8)^2-64 =225\\
&\Rightarrow (w+8)^2=289\\
&\Rightarrow (w+8)=\pm17\\
&\Rightarrow w=\pm17 - 8\end{align}$
$w$ must be positive, so $w=17-8=9$.
Using the quadratic formula
$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$
$w$ is the variable $x$, and $a=1$, $b=16$, $c=-225$
$\begin{align}w&=\dfrac{-16\pm\sqrt{16^2+4\times225}}{2}\\
&=-8\pm\sqrt{16\times4+225}\\
&=-8\pm\sqrt{289}\\
&=-8\pm17\end{align}$
Need width to be positive so $w=-8+17=9$
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
2-digit Square
A 2-Digit number is squared. When this 2-digit number is reversed and squared, the difference between the squares is also a square. What is the 2-digit number?
Consecutive Squares
The squares of any 8 consecutive numbers can be arranged into two sets of four numbers with the same sum. True of false?
Plus Minus
Can you explain the surprising results Jo found when she calculated the difference between square numbers?

