Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Window Frames



The windows in my house have six panes of glass. They are three panes wide and two panes high.

Here is a simplified drawing of a window in my house. Can you see how many small pieces of edging it uses?
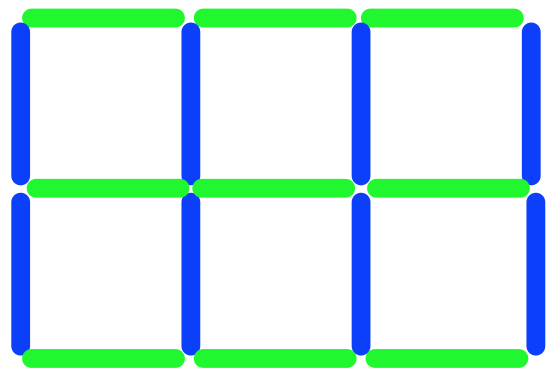
The pieces of frame go around the edge of the panes, so we call them 'edging pieces'. They are all the same length and there are 17 of them.
The picture above shows the edging pieces - there are 9 green pieces going across and 8 blue pieces going up.
Challenge 1
Explore other rectangular windows which are one window pane wider than they are high.
How many edging pieces do you need? (We need 17 in the example above.)
How many panes of glass are there altogether? (There are 6 in the example above.)
Explore the numbers you get as you make the windows bigger.
Challenge 2
In this picture, we can see the inside edging pieces coloured blue and the ones surrounding the shape coloured green:
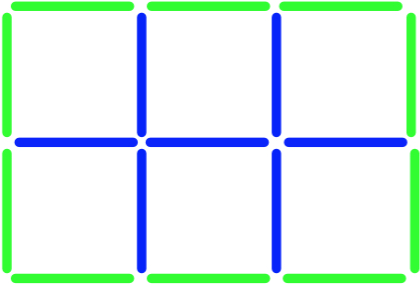
This gives us 7 inside blue pieces and 10 surrounding green pieces, making 17 altogether.
Have another look at the rectangular windows from Challenge 1, which are one window pane wider than they are high.
What numbers can you get for the inside and surrounding pieces?
Using the numbers you've got from exploring rectangular windows (that are one wider than they are high), what things can you find out about those numbers? Below you can see how others started exploring.
This idea from Louis uses sloping lines:
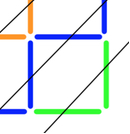
Freya used her tables knowledge:
Petros used this idea for the areas of the windows:
Kia found a different way of looking at the little squares:
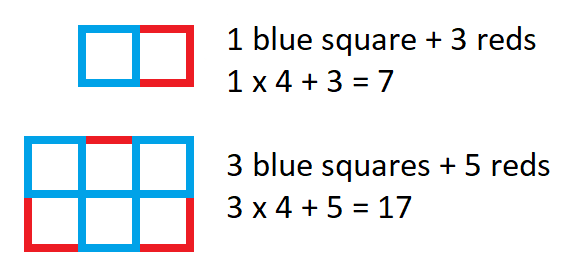
You may also like
Geoboards
This practical challenge invites you to investigate the different squares you can make on a square geoboard or pegboard.

