Skip over navigation
This activity follows on from World of Tan 24 - Clocks.
School is over for the week. In the yard, the workers are getting ready to go home. Little Fung and Little Ming are getting in the way as usual, but their puzzle has captured the attention of the supervisor, Chi Wing. They are making shapes using five small squares on a grid.
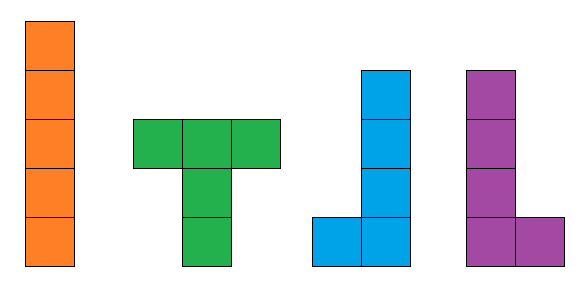
Little Ming: The teacher says there are eighteen different shapes!
Chi Wing: That might be true, but I don't believe it.
Little Fung: If the squares are joined together properly there are eighteen - she said so.
Chi Wing: Have you found them?
Little Ming and Little Fung pause and look at each other.
Chi Wing: No you haven't! I don't think you have anywhere near eighteen solutions. You two never work systematically at anything.
Little Ming: We do have seven though...
Chi Wing: Listen, what exactly were you asked to do? Little Fung, please can you explain.
Little Fung: Each shape is made up of five squares.
Little Ming: They always have to be five squares!
Chi Wing: Let Little Fung finish explaining. Little Fung, carry on please.
Little Fung: The squares have to be joined in a special way, edge to edge.
Little Ming: Yes, not corner to corner or...
Chi Wing: Little Ming, you must be quiet and let Little Fung finish.
Little Fung: The edges must be completely touching each other.
Chi Wing: Okay, I think I understand. Can you both show me what you've done so far?
Little Ming and Little Fung show Chi Wing their shapes on the squared paper.
Chi Wing: So if we move them around systematically we should be able to find the eighteen different ones.
Little Fung: Yes... but we can only find seven...
Chi Wing: Let's start again at the beginning with all the squares in a line.
Little Ming: Okay, let's begin by moving one square at a time.
Chi Wing: So which square should we start with?
Little Fung: Does it matter?
Little Ming: Yes, we need to be systematic like Chi Wing was saying, so that we can find all the possibilities.
Chi Wing: So instead of bickering, which square should we start with?
In the meantime, complete the silhouettes of Chi Wing studying the problem, then working systematically.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
World of Tan 25 - Pentominoes
Age 7 to 11
Challenge Level 





- Problem
- Teachers' Resources
This activity follows on from World of Tan 24 - Clocks.
School is over for the week. In the yard, the workers are getting ready to go home. Little Fung and Little Ming are getting in the way as usual, but their puzzle has captured the attention of the supervisor, Chi Wing. They are making shapes using five small squares on a grid.
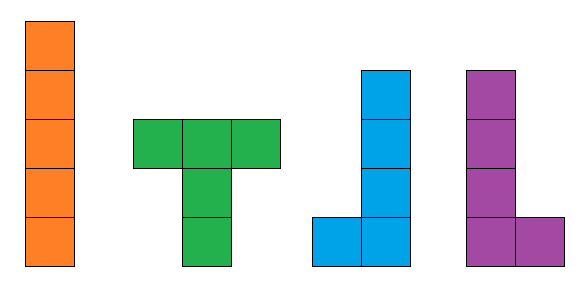
Little Ming: The teacher says there are eighteen different shapes!
Chi Wing: That might be true, but I don't believe it.
Little Fung: If the squares are joined together properly there are eighteen - she said so.
Chi Wing: Have you found them?
Little Ming and Little Fung pause and look at each other.
Chi Wing: No you haven't! I don't think you have anywhere near eighteen solutions. You two never work systematically at anything.
Little Ming: We do have seven though...
Chi Wing: Listen, what exactly were you asked to do? Little Fung, please can you explain.
Little Fung: Each shape is made up of five squares.
Little Ming: They always have to be five squares!
Chi Wing: Let Little Fung finish explaining. Little Fung, carry on please.
Little Fung: The squares have to be joined in a special way, edge to edge.
Little Ming: Yes, not corner to corner or...
Chi Wing: Little Ming, you must be quiet and let Little Fung finish.
Little Fung: The edges must be completely touching each other.
Chi Wing: Okay, I think I understand. Can you both show me what you've done so far?
Little Ming and Little Fung show Chi Wing their shapes on the squared paper.
Chi Wing: So if we move them around systematically we should be able to find the eighteen different ones.
Little Fung: Yes... but we can only find seven...
Chi Wing: Let's start again at the beginning with all the squares in a line.
Little Ming: Okay, let's begin by moving one square at a time.
Chi Wing: So which square should we start with?
Little Fung: Does it matter?
Little Ming: Yes, we need to be systematic like Chi Wing was saying, so that we can find all the possibilities.
Chi Wing: So instead of bickering, which square should we start with?
In the meantime, complete the silhouettes of Chi Wing studying the problem, then working systematically.
Extra activities:
- Find the eighteen shapes that Little Ming and Little Fung are searching for.
- How many of these shapes could be folded up to make boxes?
- Which of these shapes are reflections of each other?
- What if Little Ming and Little Fung had used six squares instead of five? How many shapes would they be able to make? How many of these shapes could be folded up to make boxes with lids?
You may also like
Little Boxes
How many different cuboids can you make when you use four CDs or DVDs? How about using five, then six?

