Rod Area
Rod Area
For this task, imagine using a number of rods, each with a length of 1 unit.
You will use the rods to create a letter U shape which is symmetrical.
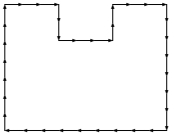
Example 1:
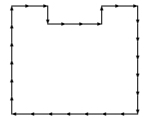
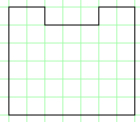
28 rods U shape Area of 39 square units
Example 2:
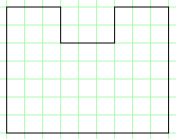
The following are not allowed as they are not U-shaped:
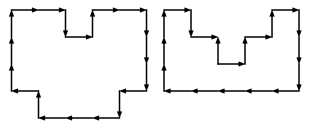
Challenge 1
Challenge 2
Can you find all the U shapes with an area of 14 square units?
How do you know you've got them all?
Here is a printable sheet of the activity.
Why do this problem?
This task was used in an Explore Learning Mathematicians' Award challenge, so it is ideal for groups of four pupils working together. The task provides a great opportunity for learners to explore the relationships between perimeter and area. If you are looking for a task in which pupils have to follow instructions/rules carefully then this would be very appropriate.
Possible approach
Set the scene for the group by explaining that we are going to make symmetrical U shapes out of small rods. Show the first example, without the numerical information if you can, and ask learners how many rods have been used, and what the area of the U shape is. Give them time to talk in pairs, then bring everyone together to confirm. You could do the same with the second example.
Then, invite learners to create their own symmetrical U shape using any number of rods. Some may wish to use some sort of manipulative (e.g. headless matches or lolly sticks), others will prefer to draw their shape. Having squared paper available will be useful. Ask learners to write down the number of rods they have used and the area of the shape, then show their shape to a partner who can check.
You could share the images of the two shapes that are not U shapes at this point to help clarify what is, and what is not, 'allowed'. If necessary, emphasise that right-angled corners always follow the edges of the square grid and rehearse some ways of finding the area using the squares as units.
You can now set learners off on the challenges. It might be helpful to print off copies of this sheet so that groups can progress at their own pace. As you walk around the room, listen out for noteworthy points to share with the whole class, for example recording strategies, ways of working systematically, efficient ways of calculating area etc.
Key questions
Tell me about this U shape.
How are you finding more than one?
How are you counting the rods?
Possible support
Some pupils may wish to use some sort of manipulative such as headless matchsticks so they can physically build some U shapes. Squared paper may be useful for recording.
Possible extensions
What do you think would happen with 21 or 22 rods instead of 20?
What would be the smallest number of rods that would allow you to find at least 8 U shapes?
You may also like
Geoboards
This practical challenge invites you to investigate the different squares you can make on a square geoboard or pegboard.
