Tables Teaser

Well done to everybody who got all of the grid headings correct! Lots of children sent us pictures of their finished grid, but only a few children explained their methods for completing it. 

Bella from the British Vietnamese International School in Vietnam explained how the times table grid works:

How this table will work is the numbers on the row on the top will multiply with each number in the column in the left, for example if the first number on the the row is 4 and the first number on the column is 5 then take 4x5 and the answer is 20 then write 20 down in the grid under 4 and next to 5. Continue that with different numbers to finish the grid.

Well done, Bella - it's always a good idea to make sure that you understand how the grid works before trying to solve it. 

Dhruv from Pict Model in India explained how he approached this problem:

First, I chose a random box and clicked on it. Then, when the number came I thought if it came in the table of 5 or 10. If a number came that was in the 5 times table I took the 5 digit and put it in the column and the row. If a number came that was in the 10 times table I will put a 10 digit in the row and the digit in the column that was in tens place in the number.

Thank you for sending us this explanation, Dhruv, and well done for looking at the numbers carefully to work out which times table they might be in. Will it always work if you put 10 as the row header and the other multiple as the column header?

Jil sent us a photo of her Tables Teaser grid, just before she clicked to show the solution:

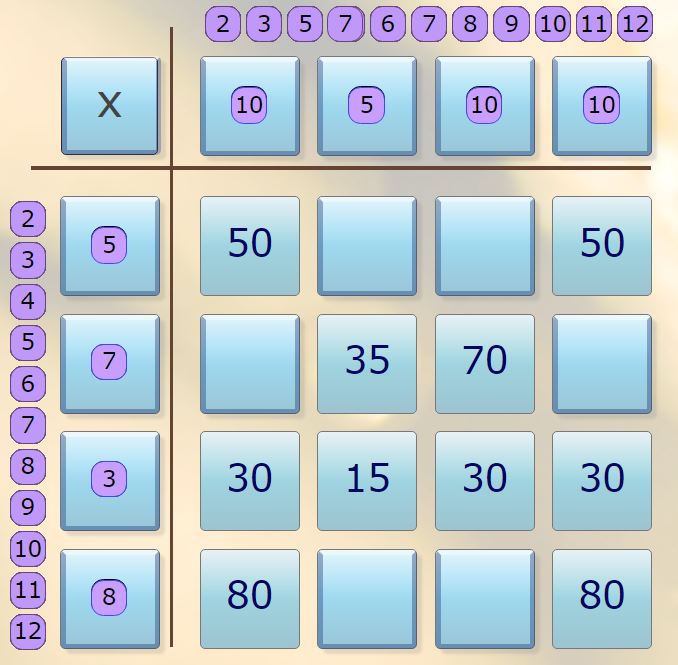
Jil said:

I opened a few numbers. I then tried to understand what is common between those numbers (that are in the same column and row). I then understood that there is a pattern between the numbers in each row and column and placed the numbers according to those patterns.

Thank you for sending in this explanation! I wonder if Jil could have solved this by clicking on fewer than 10 squares?

Gia Han found all of the grid headings by only using 7 reveals:

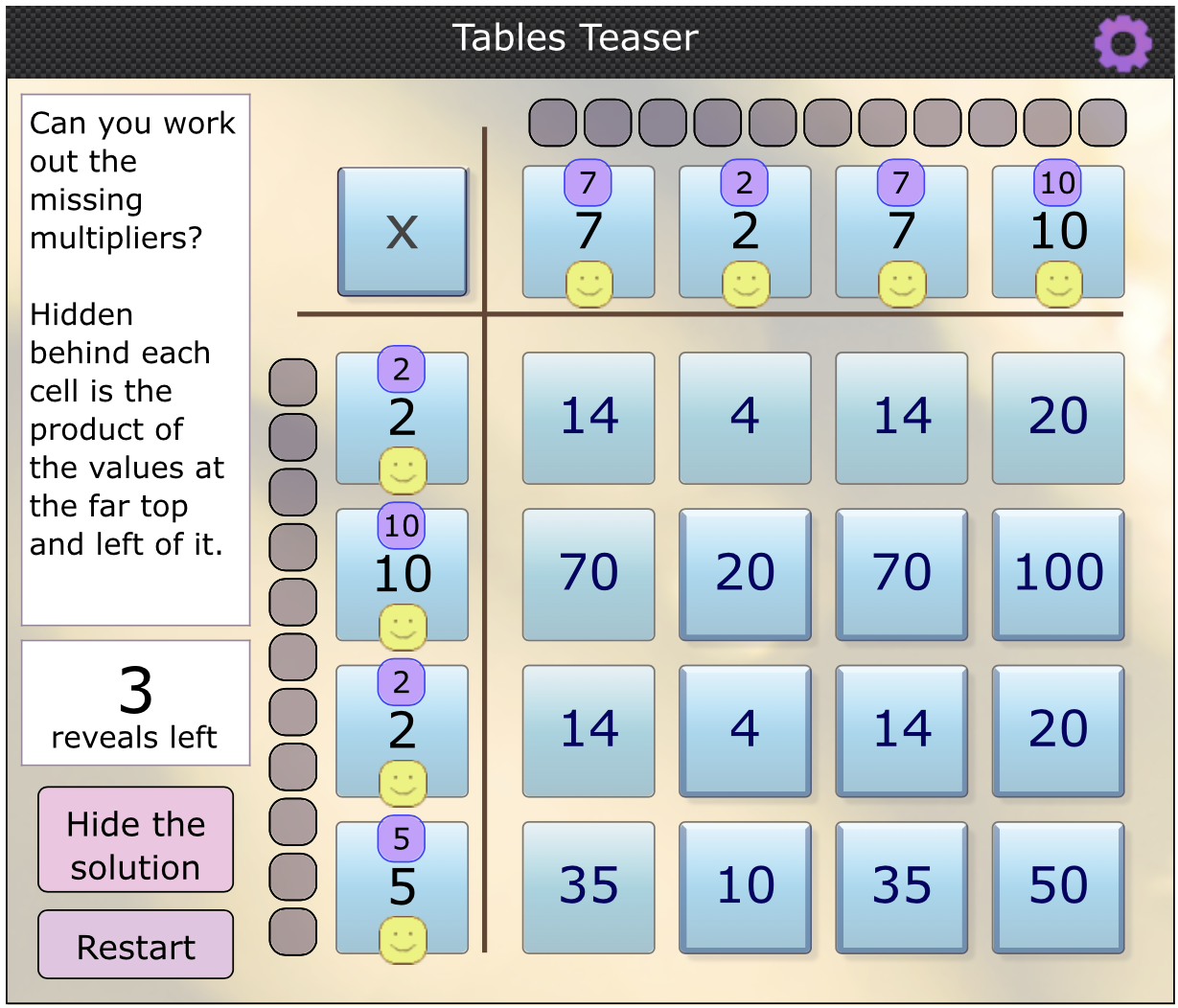
Well done! If you look closely, you can see that the numbers along the top and down the left-hand side have all been revealed. Skyler from Westridge also used this strategy:

You need to reveal all the numbers on the edge, that are next to the numbers you need to discover. Then you find the first multiples and work from there.

This is a good idea, Skyler. I wonder if you could choose to reveal all of the numbers along the bottom and down the right-hand side instead of the numbers next to the grid headings - would this strategy be different?

Jannah from ABQ Education Group in Oman also chose to reveal the numbers along the top and down the left-hand side, and she explained her reasoning in this video:

Good ideas, Jannah - I like how you looked carefully at which numbers could multiply together to give each of the numbers that you revealed.

Issa, Saja and Mohammed from ABQ Education Group in Oman each managed to solve the grid by only revealing six numbers, so they still had four reveals left at the end. I wonder what the smallest number of reveals possible is if you want to work out all of the grid headings without guessing... Would the smallest number of reveals change depending on the numbers you reveal in the grid?