Surprising Split

A large number of submissions described the mathematics behind the split and why it works.

Gold Class at Grayshott CE Primary sent in the following:
We tried it for lots of numbers and we found that it works for all double digit numbers.
We think it works because if you split 11 you get 10 and 1. So when you times the number 54 by 10, you get 540 and when you times the 54 by 1 then it's like you're ADDING another 54 onto the 540. So in the tens column you have 5 + 4 which is 9.

Isaac and Reuben from Garras C.P School wrote:
This works with all two-digit numbers.
If you do any three-digit number multiplied by eleven you can put the number you get (by adding your split numbers) either side of the the first two split numbers (and then you can get the correct answer) but you can also get it wrong if you put the number on the wrong side.

 

Crane Class from Larkrise Primary, Oxford sent their explanation and also considered decimals and three-digit numbers:
We tested it lots of times and found that the trick works for two-digit numbers where the digits add up to <10.

Paddy, Dai Dai, Zulekha and Ottilie worked together to work out that you can make it work for numbers where the digits sum >10. When you have a two digit total, use the 'ones' as the middle number and add the tens on to the left hand number. See the picture:




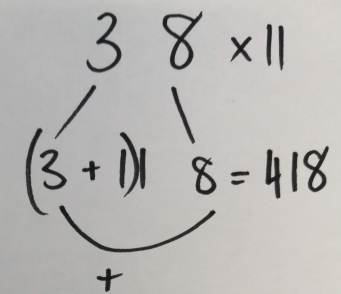
William wondered if it worked for three digit numbers... It didn't!
Mustafa wondered if it would work for decimal numbers. It did, as long as you put the decimal point back in to the right of the total in the middle.
Zulekha noticed that you could use the trick to multiply numbers by 11, then double them or quadruple them etc to find x22/33/44/55/66/77/88/99!


Lucas from The British School in the Netherlands used some algebra to generalise a solution. Here he shows his working:

 

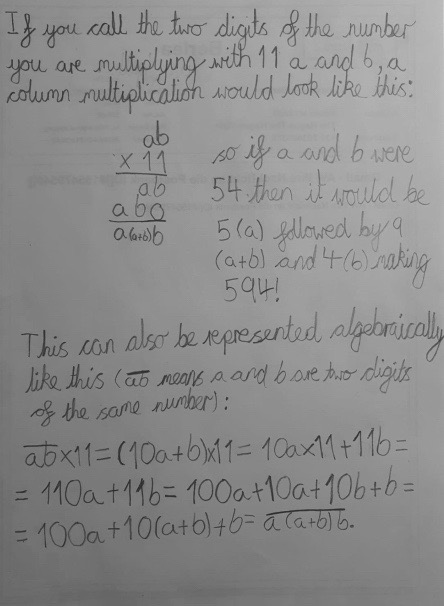
Orphée, who is home schooled, sent in the following, which also includes some ideas about three-digit numbers:
 
 
 

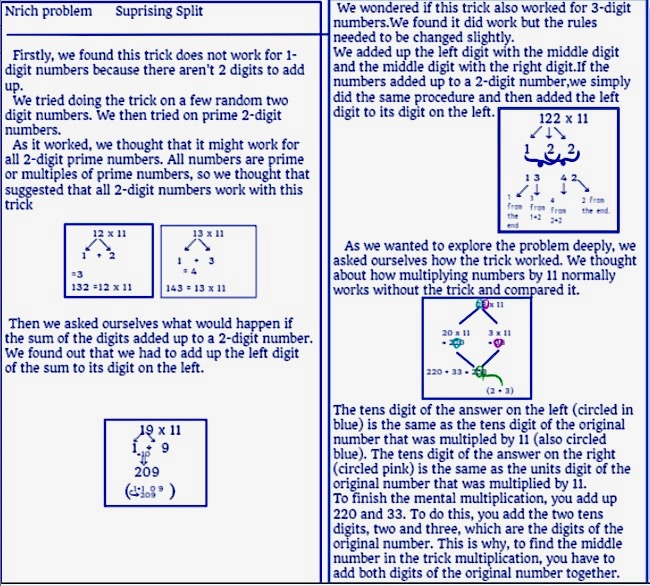
Thank you for these solutions. if you come across this task again and have a different kind of solution then do send it in.