Skip over navigation
Article by Ems Lord
Good thinkers are curious and ask good questions. They are excited by new ideas and are keen to explore and investigate them. How do we encourage our learners to become more curious mathematicians? What would we expect from a novice compared to an expert? How might we support our learners' progress towards the expert level? At NRICH, we've been working with teachers to develop and refine a collection of resources for nurturing curiosity. Let's begin by exploring our curiosity scale.
Each of the four steps in our scale describes some of the behaviours that we might expect to see from learners working at that level. We recognise that it is unlikely that they will progress smoothly from one step to the next, they might fluctuate between them; we find that this scale is most effective when it is based on a number of classroom observations:
When looking at these solutions, we are assuming that the learners were able to communicate their curiosity in a written form that was understandable by another without any verbal interpretation from the learner themselves. In the classroom we are likely to find out much more about curiosity and problem-posing skills through listening to our learners' mathematical talk as they work.
Here's a solution submitted by Tiago from the Orchards School:

He writes: "It is a triangle. It has 3 sides. 2 triangles together made a square and then we put this on the other two triangles and it made a larger triangle.It has one line of symmetry." From his written notes, we might decide that Tiago's willingness to describe his shape offers evidence of working at the 'noticing' step. Since his solution appears to feature a single shape, we are unsure whether Tiago is curious about making more shapes using his four triangles. To develop his question-posing skills, and support his progress to the next level, we might encourage him to use sentence openers such as "I wonder if..." Or, we could prompt him to suggest "questions that his mathematics teacher might ask."
We might also note that Tiago's solution mentions symmetry but he does not appear to wonder about making other shapes with the same or more lines of symmetry. When observant learners struggle to ask ther own questions, teachers tell us that they find using partial solutions from NRICH can support those learners to become more curious by realising that other learners have found more than one solution.
How does Tiago's solution compare to Zac and Olly's?
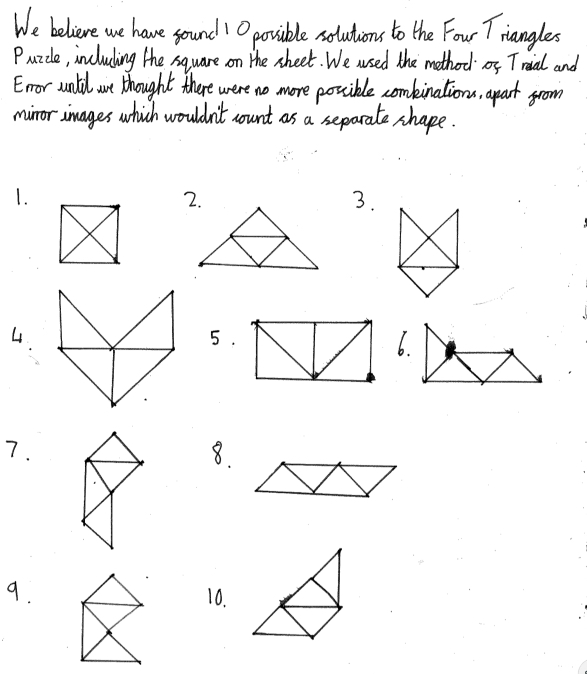
We might say that their 10 different solutions provide evidence of Zac and Olly being curious learners who keep exploring until they had found all possible answers. Their work and accompanying notes highlight their resilience, "We used the method of trial and error until we thought there were no more possible combinations apart from mirror images which would not count as a separate shape." It appears that Zac and Olly are effective problem-solvers but they are not necessarily problem-posers too. Teachers tell us that some of their learners working on this activity become curious about knowing the mathematical names for their shapes, and the subsequent conversations often lead to the learners wondering about regular and irregular shapes as they attempt to refine their vocabulary.
Another useful strategy for stimulating curiousity, and especially problem-posing, simply requires encouraging learners to alter one aspect of the original problem. For the Four Triangles Puzzle, Zac and Olly could consider increasing the number of triangles. Or, they might replace the isosceles triangles with another shape such as regular hexagons. They could also be encouraged to reflect on their approach towards solving the problem, perhaps by asking them to suggest a hint for another learner struggling with a similar problem.
Let's now look at a solution sent in by Maya, Kyra and Amelie from the Orchards School:

They write: "We noticed that a lot of the shapes were square based although we're not sure if we found all of these (8) and some were parallelogram based (5). Some were both and we got confused as to how we should group them. We noticed there were 5 quadrilaterals. We found 1 triangle. We found 6 hexagons. We found 2 pentagons." Their recording indicates that this trio of curious learners were observant and willing to ask their own questions, going beyond the remit of the original question by trying to categorise their answers yet realising "we're not sure if we've found them all" and wondering "how we should group them." Their notes also show that they investigate whether there are any more possible shapes. "We discovered we couldn't make any shapes with more than 6 sides. Amelie thought this was because as we're using 4 triangles - only two sides or less can be part of the perimeter and 2 x 4 + 8. However, a shape must have at least 2 triangles where only one side makes up the perimeter or at least one triangle where none of the sides add to the perimeter. This takes away 2 sides of the perimeter leaving you with 8-2 = 6. We wondered if there was a rule or pattern we hadn't spotted as we are not convinced we have found them all!" We might suggest that Maya, Kyra and Amelie are operating towards the higher end of the curiosity scale. Their work shows evidence of both problem-solving as well as problem-posing. As before, they might be encouraged to become even more curious learners by devising their own problems.
Some learners might display different levels of curiosity for different strands of the mathematics curriculum; some teachers tell us that their learners are more likely to be curious about shapes, measures and statistics rather than number and algebra. Investigating this further, we find that some learners hold negative attitudes towards number and algebra which possibly hinder their willingness to engage with problem-solving and problem-posing activities. Nevertheless, we believe that well designed resources can begin to oversome such hurdles. More specifically, we find that 'wow' moments, exploring manipulatives and choosing low threshold high ceiling activities all support the development of more curious learners.
'Wow' moments
Supporting students to move from problem-solving to problem-posing is a key step for nurturing more curious learners. In this article, we have already drawn attention to some tried-and-tested strategies for stimulating curiosity, such as using the stem question 'I wonder if...' and encouraging learners to consider questions that "their mathematics teacher might, or might not, ask" their classes. Researchers suggest using familiar contexts for rehearsing problem-posing skills. For example, using the context of the school canteen, learners might ask whether "their lunches are too expensive or what the most and least favorite lunches are. Others might ask how many trays are used or how many cartons of milk are sold" (Kilpatrick et al. 2001, p. 145). Once their curiosity has led to a list of questions to investigate, they will hopefully be sufficiently curious to want to go ahead and attempt to solve them too.
We find that provoking a response can be another very useful strategy for stimulating curiosity. Surprising results, which we tend to refer to as 'wow' moments, can often grab the attention of learners and they will want to understand why they happened. At NRICH we have developed a collection of activities designed to provide 'wow' moments for both primary and secondary learners. Let's explore one of the solutions for the number and algebra activity Your Number Is. This activity offers learners an interactive version of 'Think of a number' type of activities. Looking at the Teacher Resources for the activity, we see that a lesson might begin with the whole-class following the on-screen instructions, such as:
Add 3
Double
Add 4
Halve
Take away the number you started with
What did you end up with?
Try the activity for yourself a couple of times before reading any further.
We hope you, and your classes, will experience a 'wow' moment for yourselves when discovering that we always reach the same number, whatever our starting point. Moreover, encouraging our learners to be even more curious by exploring fractions, decimals and negative numbers will hopefully lead them towards wanting to understand what is happening when they keep getting the same answers.
Let's consider Elifsu's solution from the International School Laren in the Netherlands. She tries to explain what she's noticing about her answers using algebra:
Your chosen number: n
Add 3: n + 3
Double: 2n + 6
Add 4: 2n + 10
Halve: n + 5
Take away n: 5
As you can see, Elifsu notices that she keeps getting the same answer and works algebraically to explain why it happened. She does not stop there, Elifsu creates two examples of her own:
Example One
Choose a number
Multiply by 2
Add 10
Divide by 2
Subtract the number you started with
Start again?
Example Two
Choose a number
Multiply by 2
Add 26
Divide by 2
Subtract the number you started with
Comparing her two examples, what does Elisfu keep the same? What does she change? For the first example, Elisfu uses the numbers 10 and 5 and for the second example so chooses 26 and 13. We suggest that her example hints at her understanding of a general method for solving and posing these types of problems.
Hopefully, the on-screen prompts also lead Elisfu to explore fractions and negative numbers too. Once learners have enjoyed exploring the activity Your Number Is, perhaps writing their own similar problems like Elisfu too, they might like to explore The Number Jumbler which also offers learners a 'wow' moment through an interactive activity.
Maximising the potential of hints, prompts and manipulatives for nurturing curiosity
Earlier in this article we suggested that curious learners might benefit from writing hints to help others to become more curious too. As we saw with the above activity, NRICH resources often model this approach by enabling learners to click on hints as they work through a problem. A useful set of resources are our primary and secondary 'I wonder...what if...?' collections. They include Number Sandwiches and More Number Sandwiches which make excellent use of hints to stimulate curiosity throughout the activity:
In this arrangement there is one number sandwiched between the "1" cards, two numbers sandwiched between the "2" cards, but only one number sandwich between the "3" cards.

Is it possible to make a complete sandwich with one number between the "1" cards, two numbers between the "2" cards, and three numbers between the "3" cards? Click to reveal an interactivity that might help you to explore...
Looking at the solutions we received at NRICH, it appears that the hints and prompts enable learners to behave in a curious manner as they worked their way through this problem. Here's Emily's solution from the Burford School:
"The first problem [using the numbers 1,2 and 3] required logic. I knew that the threes could fit around the ones' sequence. That only left two twos. I placed a two in between the ones - as the middle number. Then I could only experiment with the remaining card - a two. I tried the two in every possible place and came out with two sequences - 231213 and 312132."
At this point, Emily is sufficiently curious to follow the on-screen prompt encouraging her to explore a more challenging version of the problem using four digits rather than three:
"The second problem required more than just logic. I used the aid of the interactivity for this problem. I knew that the ones' and twos' sequence could fit inside the fours. I tried that, but it didn't work as the ones and twos overlapped other numbers. I slid the ones beside the fours, then I put the twos in the possible places - only one worked. The gaps left were three spaces apart - perfect for the threes. I came out with the sequence - 41312432."
Her solution shows the benefits of working with either digital or hand-held interactives for stimulating mathematical curiosity; by engaging with the onscreen interactivity, Emily is able to explore different ideas and reach a solution for four digits. Not content at that point, she was prompted by the on-screen hint to attempt five digits:
"The third problem was a bit of a mind teaser. Luckily, I had spotted a pattern - all the sequences started with the highest number, followed by a one. I put the seven and the one in these places and then I examined the sequences again. The sequences had a three in between the ones! I slotted the threes in the middle of the ones. I thought about the problem. I realised that the highest numbers would be early in the sequence, as they required more space in between them. The highest number left was six. I placed the sixes in the next possible place. Then I dealt with the fives. I slotted them in next to the sixes, but the last five and last six required the same space. So, I tried the next available space for the fives and it fitted. The next challenge was the fours. I did what I did for the last numbers. I placed the fours in the first available space - luckily it fitted. That left two spaces, two spaces apart. I slotted the only remaining cards in the remaining spaces - the twos. Finally, I had the sequence - 71316435724625."
Emily's solution highights the benefits of using scaffolded digital resources for nurturing mathematical curiosity. Their step-by-step approach enables her to engage with a challenging problem demanding resilience and perseverance to reach a solution. We hope that she extends her investigation further, perhaps considering larger number sandwiches or generalising her results. You can read our article exploring the benefits of using digital manipulatives in the classroom here, and we have published a set of accompanying primary and secondary resources.
Curiosity and setting an appropriate level of challenge
We find that there appeared to be differing views regarding the level of challenge required for stimulating curiosity among learners. With some classes, teachers report that they need to pose very challenging problems to engage the curiosity of some of their learners. However, that is not usually the case and other teachers tell us that they often choose activities intended for younger learners. The level of maths challenge for NRICH problems is indicated by a scale of one, two or three stars.
* Problems that require some initial investigation and planning,
** Problems that extend beyond normal curriculum demands and which challenge learners working at the next stage,
*** Very challenging problems.
The chart gives some guidance on which problems may be most appropriate for pupils at various ages and levels of attainment (please note that 'Stage 1' refers to 'Key Stage 1' and so on):
At NRICH, we try to offer as much flexibility to learners and teachers as possible and to discourage the view that a problem that uses curriculum content at Stage 2 is inappropriate for learners working at stages 3 or 4 (or even 1). There are three main reasons for this:
We hope that this article has highlighted a selection of classroom-based approaches suitable for nurturing more curious learners who ask good questions. Using 'wow' moments, offering hints and encouraging learners to explore manipulatives are useful approaches towards stimulating mathematical curiosity as well as choosing LTHC activities. Moreover, we have also shared our four step progression for supporting learners to become more curious in their mathematics classroom. If you would like to explore more of our curiosity activities, and our other resources encouraging learners to develop mathematical Habits of Mind, please do take a look at our primary and secondary 'Being Curious' collections where we have organised the resources into curriculum strands addressing number and algebra, statistics, measures and geometry.
References
Kilpatrick, J., Swafford, J., & Findell, B. (Eds.). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academies Press.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Age 7 to 18
Published 2019 Revised 2020
Curiosity: the Journey from Novice to Expert
This article reports findings from part of a wider NRICH project addressing ways to nurture and develop curiosity in the classroom.
Nurturing curiosity
Good thinkers are curious and ask good questions. They are excited by new ideas and are keen to explore and investigate them. How do we encourage our learners to become more curious mathematicians? What would we expect from a novice compared to an expert? How might we support our learners' progress towards the expert level? At NRICH, we've been working with teachers to develop and refine a collection of resources for nurturing curiosity. Let's begin by exploring our curiosity scale.
Progression in curiosity
Each of the four steps in our scale describes some of the behaviours that we might expect to see from learners working at that level. We recognise that it is unlikely that they will progress smoothly from one step to the next, they might fluctuate between them; we find that this scale is most effective when it is based on a number of classroom observations:
- Step One: Noticing: these learners tend to describe what they see, often benefiting from prompts such as 'What's the same, what's different?'
- Step Two: Wondering: these learners are beginning to ask their own questions, perhaps using prompts such as "I wonder if..." or asking "What might a mathematician ask...?"
- Step Three: Investigating: these learners are problem-solvers, often drawing on their resilience and perseverance when they get stuck, make a mistake or need to try a different approach
- Step Four: Reflecting and Creating: these curious learners are both problem-solvers and problem-posers, they might devise a new problem to investigate by tinkering with an earlier challenge, and they might reflect on their learning and suggest hints for others to help them investigate similar problems.
If you cut a square diagonally from corner to corner you get four right-angled isosceles triangles.

How many different shapes can you make by fitting the four triangles back together?
You may only fit long sides to long sides and short sides to short sides.
The whole length of the side must be joined.

How many different shapes can you make by fitting the four triangles back together?
You may only fit long sides to long sides and short sides to short sides.
The whole length of the side must be joined.
When looking at these solutions, we are assuming that the learners were able to communicate their curiosity in a written form that was understandable by another without any verbal interpretation from the learner themselves. In the classroom we are likely to find out much more about curiosity and problem-posing skills through listening to our learners' mathematical talk as they work.
Here's a solution submitted by Tiago from the Orchards School:

He writes: "It is a triangle. It has 3 sides. 2 triangles together made a square and then we put this on the other two triangles and it made a larger triangle.It has one line of symmetry." From his written notes, we might decide that Tiago's willingness to describe his shape offers evidence of working at the 'noticing' step. Since his solution appears to feature a single shape, we are unsure whether Tiago is curious about making more shapes using his four triangles. To develop his question-posing skills, and support his progress to the next level, we might encourage him to use sentence openers such as "I wonder if..." Or, we could prompt him to suggest "questions that his mathematics teacher might ask."
We might also note that Tiago's solution mentions symmetry but he does not appear to wonder about making other shapes with the same or more lines of symmetry. When observant learners struggle to ask ther own questions, teachers tell us that they find using partial solutions from NRICH can support those learners to become more curious by realising that other learners have found more than one solution.
How does Tiago's solution compare to Zac and Olly's?

We might say that their 10 different solutions provide evidence of Zac and Olly being curious learners who keep exploring until they had found all possible answers. Their work and accompanying notes highlight their resilience, "We used the method of trial and error until we thought there were no more possible combinations apart from mirror images which would not count as a separate shape." It appears that Zac and Olly are effective problem-solvers but they are not necessarily problem-posers too. Teachers tell us that some of their learners working on this activity become curious about knowing the mathematical names for their shapes, and the subsequent conversations often lead to the learners wondering about regular and irregular shapes as they attempt to refine their vocabulary.
Another useful strategy for stimulating curiousity, and especially problem-posing, simply requires encouraging learners to alter one aspect of the original problem. For the Four Triangles Puzzle, Zac and Olly could consider increasing the number of triangles. Or, they might replace the isosceles triangles with another shape such as regular hexagons. They could also be encouraged to reflect on their approach towards solving the problem, perhaps by asking them to suggest a hint for another learner struggling with a similar problem.
Let's now look at a solution sent in by Maya, Kyra and Amelie from the Orchards School:

They write: "We noticed that a lot of the shapes were square based although we're not sure if we found all of these (8) and some were parallelogram based (5). Some were both and we got confused as to how we should group them. We noticed there were 5 quadrilaterals. We found 1 triangle. We found 6 hexagons. We found 2 pentagons." Their recording indicates that this trio of curious learners were observant and willing to ask their own questions, going beyond the remit of the original question by trying to categorise their answers yet realising "we're not sure if we've found them all" and wondering "how we should group them." Their notes also show that they investigate whether there are any more possible shapes. "We discovered we couldn't make any shapes with more than 6 sides. Amelie thought this was because as we're using 4 triangles - only two sides or less can be part of the perimeter and 2 x 4 + 8. However, a shape must have at least 2 triangles where only one side makes up the perimeter or at least one triangle where none of the sides add to the perimeter. This takes away 2 sides of the perimeter leaving you with 8-2 = 6. We wondered if there was a rule or pattern we hadn't spotted as we are not convinced we have found them all!" We might suggest that Maya, Kyra and Amelie are operating towards the higher end of the curiosity scale. Their work shows evidence of both problem-solving as well as problem-posing. As before, they might be encouraged to become even more curious learners by devising their own problems.
Some learners might display different levels of curiosity for different strands of the mathematics curriculum; some teachers tell us that their learners are more likely to be curious about shapes, measures and statistics rather than number and algebra. Investigating this further, we find that some learners hold negative attitudes towards number and algebra which possibly hinder their willingness to engage with problem-solving and problem-posing activities. Nevertheless, we believe that well designed resources can begin to oversome such hurdles. More specifically, we find that 'wow' moments, exploring manipulatives and choosing low threshold high ceiling activities all support the development of more curious learners.
'Wow' moments
Supporting students to move from problem-solving to problem-posing is a key step for nurturing more curious learners. In this article, we have already drawn attention to some tried-and-tested strategies for stimulating curiosity, such as using the stem question 'I wonder if...' and encouraging learners to consider questions that "their mathematics teacher might, or might not, ask" their classes. Researchers suggest using familiar contexts for rehearsing problem-posing skills. For example, using the context of the school canteen, learners might ask whether "their lunches are too expensive or what the most and least favorite lunches are. Others might ask how many trays are used or how many cartons of milk are sold" (Kilpatrick et al. 2001, p. 145). Once their curiosity has led to a list of questions to investigate, they will hopefully be sufficiently curious to want to go ahead and attempt to solve them too.
We find that provoking a response can be another very useful strategy for stimulating curiosity. Surprising results, which we tend to refer to as 'wow' moments, can often grab the attention of learners and they will want to understand why they happened. At NRICH we have developed a collection of activities designed to provide 'wow' moments for both primary and secondary learners. Let's explore one of the solutions for the number and algebra activity Your Number Is. This activity offers learners an interactive version of 'Think of a number' type of activities. Looking at the Teacher Resources for the activity, we see that a lesson might begin with the whole-class following the on-screen instructions, such as:
Add 3
Double
Add 4
Halve
Take away the number you started with
What did you end up with?
Try the activity for yourself a couple of times before reading any further.
We hope you, and your classes, will experience a 'wow' moment for yourselves when discovering that we always reach the same number, whatever our starting point. Moreover, encouraging our learners to be even more curious by exploring fractions, decimals and negative numbers will hopefully lead them towards wanting to understand what is happening when they keep getting the same answers.
Let's consider Elifsu's solution from the International School Laren in the Netherlands. She tries to explain what she's noticing about her answers using algebra:
Your chosen number: n
Add 3: n + 3
Double: 2n + 6
Add 4: 2n + 10
Halve: n + 5
Take away n: 5
As you can see, Elifsu notices that she keeps getting the same answer and works algebraically to explain why it happened. She does not stop there, Elifsu creates two examples of her own:
Example One
Choose a number
Multiply by 2
Add 10
Divide by 2
Subtract the number you started with
Start again?
Example Two
Choose a number
Multiply by 2
Add 26
Divide by 2
Subtract the number you started with
Comparing her two examples, what does Elisfu keep the same? What does she change? For the first example, Elisfu uses the numbers 10 and 5 and for the second example so chooses 26 and 13. We suggest that her example hints at her understanding of a general method for solving and posing these types of problems.
Hopefully, the on-screen prompts also lead Elisfu to explore fractions and negative numbers too. Once learners have enjoyed exploring the activity Your Number Is, perhaps writing their own similar problems like Elisfu too, they might like to explore The Number Jumbler which also offers learners a 'wow' moment through an interactive activity.
Maximising the potential of hints, prompts and manipulatives for nurturing curiosity
Earlier in this article we suggested that curious learners might benefit from writing hints to help others to become more curious too. As we saw with the above activity, NRICH resources often model this approach by enabling learners to click on hints as they work through a problem. A useful set of resources are our primary and secondary 'I wonder...what if...?' collections. They include Number Sandwiches and More Number Sandwiches which make excellent use of hints to stimulate curiosity throughout the activity:
In this arrangement there is one number sandwiched between the "1" cards, two numbers sandwiched between the "2" cards, but only one number sandwich between the "3" cards.

Looking at the solutions we received at NRICH, it appears that the hints and prompts enable learners to behave in a curious manner as they worked their way through this problem. Here's Emily's solution from the Burford School:
"The first problem [using the numbers 1,2 and 3] required logic. I knew that the threes could fit around the ones' sequence. That only left two twos. I placed a two in between the ones - as the middle number. Then I could only experiment with the remaining card - a two. I tried the two in every possible place and came out with two sequences - 231213 and 312132."
At this point, Emily is sufficiently curious to follow the on-screen prompt encouraging her to explore a more challenging version of the problem using four digits rather than three:
"The second problem required more than just logic. I used the aid of the interactivity for this problem. I knew that the ones' and twos' sequence could fit inside the fours. I tried that, but it didn't work as the ones and twos overlapped other numbers. I slid the ones beside the fours, then I put the twos in the possible places - only one worked. The gaps left were three spaces apart - perfect for the threes. I came out with the sequence - 41312432."
Her solution shows the benefits of working with either digital or hand-held interactives for stimulating mathematical curiosity; by engaging with the onscreen interactivity, Emily is able to explore different ideas and reach a solution for four digits. Not content at that point, she was prompted by the on-screen hint to attempt five digits:
"The third problem was a bit of a mind teaser. Luckily, I had spotted a pattern - all the sequences started with the highest number, followed by a one. I put the seven and the one in these places and then I examined the sequences again. The sequences had a three in between the ones! I slotted the threes in the middle of the ones. I thought about the problem. I realised that the highest numbers would be early in the sequence, as they required more space in between them. The highest number left was six. I placed the sixes in the next possible place. Then I dealt with the fives. I slotted them in next to the sixes, but the last five and last six required the same space. So, I tried the next available space for the fives and it fitted. The next challenge was the fours. I did what I did for the last numbers. I placed the fours in the first available space - luckily it fitted. That left two spaces, two spaces apart. I slotted the only remaining cards in the remaining spaces - the twos. Finally, I had the sequence - 71316435724625."
Emily's solution highights the benefits of using scaffolded digital resources for nurturing mathematical curiosity. Their step-by-step approach enables her to engage with a challenging problem demanding resilience and perseverance to reach a solution. We hope that she extends her investigation further, perhaps considering larger number sandwiches or generalising her results. You can read our article exploring the benefits of using digital manipulatives in the classroom here, and we have published a set of accompanying primary and secondary resources.
Curiosity and setting an appropriate level of challenge
We find that there appeared to be differing views regarding the level of challenge required for stimulating curiosity among learners. With some classes, teachers report that they need to pose very challenging problems to engage the curiosity of some of their learners. However, that is not usually the case and other teachers tell us that they often choose activities intended for younger learners. The level of maths challenge for NRICH problems is indicated by a scale of one, two or three stars.
* Problems that require some initial investigation and planning,
** Problems that extend beyond normal curriculum demands and which challenge learners working at the next stage,
*** Very challenging problems.
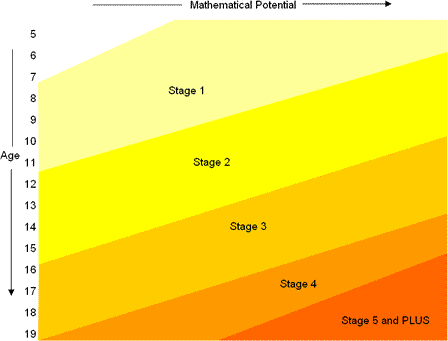
The chart gives some guidance on which problems may be most appropriate for pupils at various ages and levels of attainment (please note that 'Stage 1' refers to 'Key Stage 1' and so on):

At NRICH, we try to offer as much flexibility to learners and teachers as possible and to discourage the view that a problem that uses curriculum content at Stage 2 is inappropriate for learners working at stages 3 or 4 (or even 1). There are three main reasons for this:
- Firstly we learn at different rates, and this means that a problem which uses mathematical content normally associated with one particular stage can often successfully enable a fresh grasp of that same content at a different stage.
- The problems are designed to promote problem solving and investigative mathematics. The development of this type of thinking is not tied to levels of content knowledge.
- Finally, the problems within each stage cover between them a full range of challenge levels. A problem with a lower challenge level might offer opportunities to introduce mathematical ideas to students ahead of that content being taught in the "normal curriculum". Similarly problems at the highest challenge level can test the problem-solving skills of the most able mathematicians, despite the mathematical content resting on ideas normally met at an earlier stage.
In conclusion
We hope that this article has highlighted a selection of classroom-based approaches suitable for nurturing more curious learners who ask good questions. Using 'wow' moments, offering hints and encouraging learners to explore manipulatives are useful approaches towards stimulating mathematical curiosity as well as choosing LTHC activities. Moreover, we have also shared our four step progression for supporting learners to become more curious in their mathematics classroom. If you would like to explore more of our curiosity activities, and our other resources encouraging learners to develop mathematical Habits of Mind, please do take a look at our primary and secondary 'Being Curious' collections where we have organised the resources into curriculum strands addressing number and algebra, statistics, measures and geometry.
References
Kilpatrick, J., Swafford, J., & Findell, B. (Eds.). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academies Press.

